题目内容
【题目】已知数列{an}满足an+1= 
an+t，a1= （t为常数，且t≠ 
）．
（1）证明：{an﹣2t}为等比数列；
（2）当t=﹣ 
时，求数列{an}的前几项和最大？
（3）当t=0时，设cn=4an+1，数列{cn}的前n项和为Tn ， 若不等式 
≥2n﹣7对任意的n∈N*恒成立，求实数k的取值范围．
【答案】
（1）证明：∵数列{an}满足an+1= 
an+t，a1= （t为常数，且t≠ 
），
∴ 
，
∴ 
= ，
又a1﹣2t= 
，
∴{an﹣2t}是以 为首项，以 为公比的等比数列
（2）解：当t=﹣ 
时，{an+ }是以 
为首项，以 为公比的等比数列，
∴ 
，
∴ 
，
由 ≥0，解得n≤2．
∴数列{an}的前2项和最大
（3）解：当t=0时，∴{an}是以 为首项，以 为公比的等比数列，∴an= 
，
cn=4an+1= 
+1，
∴数列{cn}的前n项和：
Tn= 
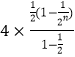=4+n﹣ ，
∵不等式 
≥2n﹣7对任意的n∈N*恒成立，
∴3k≥ 
对任意的n∈N*恒成立，
设 
，由dn+1﹣dn= 
= 
，
∴当n≤4时，dn+1＞dn，
当n≥4时，dn+1＜dn，
∵ 
，
∴3k 
，解得k 
．
∴实数k的取值范围是[ 
）
【解析】（1）由已知得 ，由此能证明{an﹣2t}是以 为首项，以 为公比的等比数列．（2）当t=﹣ 时，{an+ }是以 为首项，以 为公比的等比数列，求出 ，由此能求出数列{an}的前几项和最大．（3）当t=0时，an= ，cn=4an+1= +1，从而Tn=4+n﹣ ，由不等式 ≥2n﹣7对任意的n∈N*恒成立，得到3k≥ 对任意的n∈N*恒成立，由此能求出实数k的取值范围．
【考点精析】解答此题的关键在于理解数列的通项公式的相关知识，掌握如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
