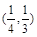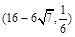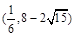题目内容
已知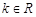 ,函数
,函数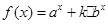
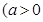 且
且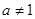 ,
,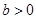 且
且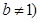 .
.
(1) 如果实数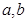 满足
满足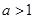 且
且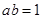 ,函数
,函数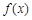 是否具有奇偶性? 如果有,求出相应的
是否具有奇偶性? 如果有,求出相应的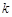 值;如果没有,说明原因;
值;如果没有,说明原因;
(2) 如果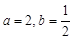 ,讨论函数
,讨论函数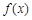 的单调性。
的单调性。
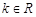 ,函数
,函数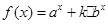
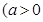 且
且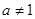 ,
,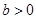 且
且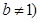 .
.(1) 如果实数
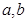 满足
满足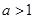 且
且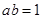 ,函数
,函数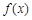 是否具有奇偶性? 如果有,求出相应的
是否具有奇偶性? 如果有,求出相应的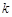 值;如果没有,说明原因;
值;如果没有,说明原因;(2) 如果
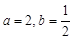 ,讨论函数
,讨论函数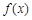 的单调性。
的单调性。(1)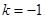 时,函数
时,函数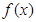 为奇函数;
为奇函数;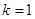 时,函数
时,函数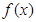 为偶函数.
为偶函数.
(2)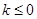 时,
时,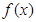 在
在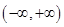 递增;
递增;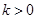 时,减区间
时,减区间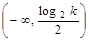 ,增区间
,增区间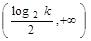 .
.
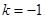 时,函数
时,函数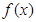 为奇函数;
为奇函数;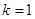 时,函数
时,函数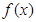 为偶函数.
为偶函数.(2)
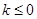 时,
时,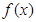 在
在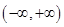 递增;
递增;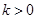 时,减区间
时,减区间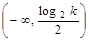 ,增区间
,增区间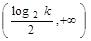 .
.试题分析:(1)因为
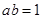 ,所以
,所以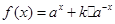 ,
,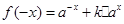 ,根据奇函数偶函数的定义即可求得k的值.(2)
,根据奇函数偶函数的定义即可求得k的值.(2)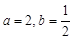 ,所以
,所以 ,
,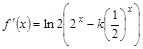 .根据导数的符号即可得函数的单调性.在本题中,由于含有参数k,故需要对k进行讨论.
.根据导数的符号即可得函数的单调性.在本题中,由于含有参数k,故需要对k进行讨论.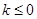 时,
时,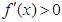 恒成立,
恒成立,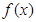 在
在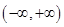 递增;
递增;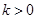 时,若
时,若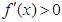 ,则
,则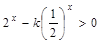 ,
,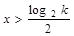 ; 若
; 若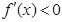 ,则
,则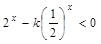 ,
,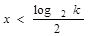 ,增区间
,增区间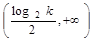 ,减区间
,减区间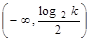 .
.试题解析:(1)由题意得:
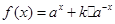 ,
,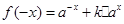 ,
, 若函数
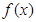 为奇函数,则
为奇函数,则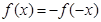 ,
,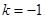 ;
;若函数
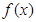 为偶函数,则
为偶函数,则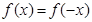 ,
,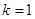 . 6分
. 6分(2)由题意知:
 ,
,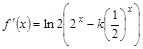 ..7分
..7分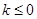 时,
时,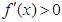 恒成立,
恒成立,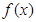 在
在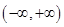 递增; 9分
递增; 9分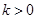 时,若
时,若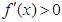 ,则
,则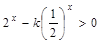 ,
,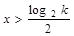
若
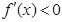 ,则
,则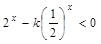 ,
,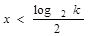
增区间
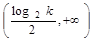 ,减区间
,减区间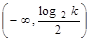 12分
12分综上:
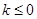 时,
时, 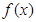 在
在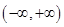 递增;
递增;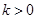 时,减区间
时,减区间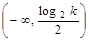 ,增区间
,增区间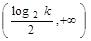 . 13分
. 13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是定义在
是定义在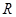 上的偶函数,当
上的偶函数,当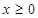 时,
时,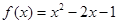 。
。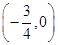 成中心对称,对任意实数x都有f(x)=-
成中心对称,对任意实数x都有f(x)=- ,且f(-1)=1,f(0)=-2,则f(0)+f(1)+…+f(2013)=________.
,且f(-1)=1,f(0)=-2,则f(0)+f(1)+…+f(2013)=________.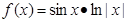 的部分图像为( )
的部分图像为( )
 是定义在
是定义在 上的奇函数,若对于任意的实数
上的奇函数,若对于任意的实数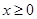 ,都有
,都有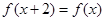 ,且当
,且当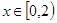 时,
时,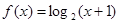 ,则
,则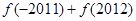 的值为( )
的值为( )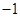
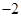
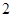
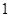
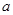 为实常数,
为实常数,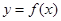 是定义在
是定义在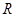 上的奇函数,当
上的奇函数,当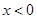 时,
时,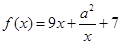 , 若
, 若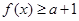 对一切
对一切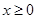 成立,则
成立,则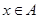 ,
,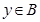 ,(
,(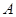 、
、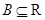 )有唯一确定的
)有唯一确定的 与之对应,称
与之对应,称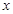 、
、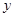 的二元函数.现定义满足下列性质的二元函数
的二元函数.现定义满足下列性质的二元函数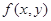 为关于实数
为关于实数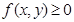 ,当且仅当
,当且仅当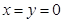 时取等号;
时取等号;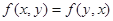 ;
;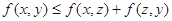 对任意的实数z均成立.
对任意的实数z均成立.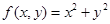 ;②
;②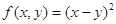 ;③
;③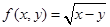 ;
;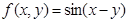 .能够成为关于的
.能够成为关于的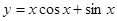 的图像大致为( )
的图像大致为( )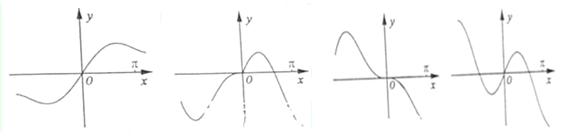
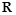 上的函数
上的函数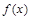 满足
满足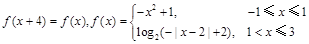 ,若关于x的方程
,若关于x的方程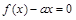 有5个不同实根,则正实数
有5个不同实根,则正实数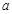 的取值范围是( )
的取值范围是( )