题目内容
对正整数n,设曲线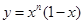 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为 ,则
,则 的前n项和是 .
的前n项和是 .

解析试题分析:易知y'=nxn-1-(n+1)xn,曲线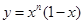 在x=2处的切线的斜率为k=n2n-1-(n+1)2n,切点为(2,-2n),所以切线方程为y+2n=k(x-2),令x=0得an=(n+1)2n,所以
在x=2处的切线的斜率为k=n2n-1-(n+1)2n,切点为(2,-2n),所以切线方程为y+2n=k(x-2),令x=0得an=(n+1)2n,所以 ,所以数列
,所以数列 是首项为2,公比为2的等比数列。所以
是首项为2,公比为2的等比数列。所以 的前n项和是
的前n项和是 。
。
考点:利用导数研究曲线上某点切线方程;导数的几何意义;等差数列的前n项和公式。
点评:应用导数求曲线切线的斜率时,要注意“在某点的切线”与“过某点的切线”的区别,否则容易出错。

练习册系列答案
相关题目
 是等差数列,
是等差数列, ,其中
,其中 ,则此数列的前
,则此数列的前 项和
项和 _______ .
_______ . ,则
,则 ;
; ;
; ,则
,则 一定有最小值.
一定有最小值. 是数列
是数列 的前
的前 项和,若
项和,若 ,则数列
,则数列 ,则
,则
 ,若存在
,若存在 ,使得
,使得 成立,则
成立,则
 中,
中, 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若 则
则 =p(p为正常数,n∈N+),则称{an}为“等方比数列”.
=p(p为正常数,n∈N+),则称{an}为“等方比数列”. 的前n项和为
的前n项和为 则三点
则三点 共线;
共线; ”的否定是“
”的否定是“ ”;
”; 在(0,1)没有零点,则k的取值范围是
在(0,1)没有零点,则k的取值范围是
 是定义在R上的奇函数,
是定义在R上的奇函数, 的解集为(
的解集为( 2,2)
2,2) 中,若
中,若 且
且 ,则数列
,则数列 ____________。
____________。 满足
满足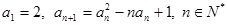 .
. ;
; 的一个通项公式,并用数学归纳法证明你的结论;(本题满分13分)
的一个通项公式,并用数学归纳法证明你的结论;(本题满分13分) ,an=
,an= (
(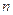 为正整数),
为正整数), ,cn=(an+19)(Sn+50),数列{cn}前n项和为Tn,
,cn=(an+19)(Sn+50),数列{cn}前n项和为Tn,