题目内容
已知函数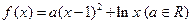
(Ⅰ)当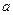 =1时,判断函数
=1时,判断函数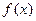 的单调性并写出其单调区间;
的单调性并写出其单调区间;
(Ⅱ)在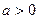 的条件下,若函数
的条件下,若函数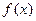 的图象与直线y=x至少有一个交点,求实数
的图象与直线y=x至少有一个交点,求实数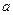 的取值范围。
的取值范围。
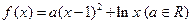
(Ⅰ)当
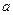 =1时,判断函数
=1时,判断函数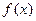 的单调性并写出其单调区间;
的单调性并写出其单调区间;(Ⅱ)在
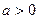 的条件下,若函数
的条件下,若函数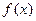 的图象与直线y=x至少有一个交点,求实数
的图象与直线y=x至少有一个交点,求实数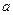 的取值范围。
的取值范围。(Ⅰ)函数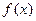 为增函数,单调增区间为
为增函数,单调增区间为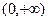 (Ⅱ)
(Ⅱ)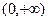
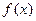 为增函数,单调增区间为
为增函数,单调增区间为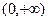 (Ⅱ)
(Ⅱ)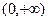
(Ⅰ)当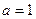 时,
时,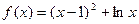 ,其定义域为
,其定义域为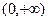
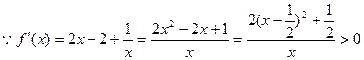
∴函数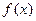 为增函数,单调增区间为
为增函数,单调增区间为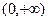 ---------6分
---------6分
(Ⅱ)设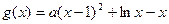 ,
,
由题意得方程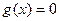 在区间
在区间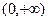 上至少有一解 ------7分
上至少有一解 ------7分
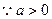
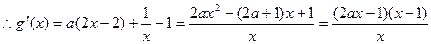
令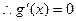 得
得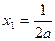 ,
,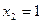 --------9分
--------9分
(1)当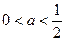 时,可得
时,可得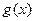 的单调增区间为
的单调增区间为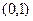 ,
,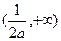 ,单调减区间为
,单调减区间为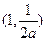
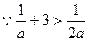 ∴极大值为
∴极大值为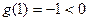 ,极小值为
,极小值为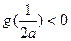
又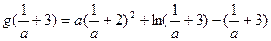
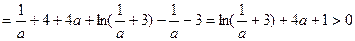
∴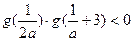 ∴方程
∴方程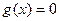 恰好有一解 -------11分
恰好有一解 -------11分
(2)当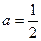 时,
时,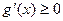 ,
,
∴函数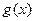 为增函数,由(1)得方程
为增函数,由(1)得方程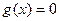 也恰好有一解 -------12分
也恰好有一解 -------12分
(3)当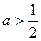 时,
时,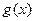 的单调增区间为
的单调增区间为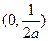 ,
,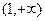 ,单调减区间为
,单调减区间为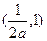
同(1)可得方程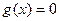 在
在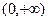 至少有一解
至少有一解
综上所述所求的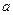 取值范围为
取值范围为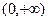 -------14分
-------14分
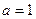 时,
时,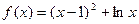 ,其定义域为
,其定义域为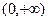
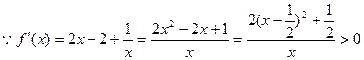
∴函数
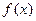 为增函数,单调增区间为
为增函数,单调增区间为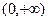 ---------6分
---------6分(Ⅱ)设
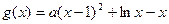 ,
,由题意得方程
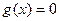 在区间
在区间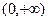 上至少有一解 ------7分
上至少有一解 ------7分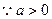
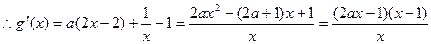
令
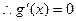 得
得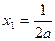 ,
,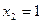 --------9分
--------9分(1)当
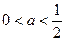 时,可得
时,可得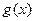 的单调增区间为
的单调增区间为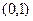 ,
,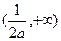 ,单调减区间为
,单调减区间为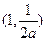
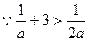 ∴极大值为
∴极大值为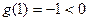 ,极小值为
,极小值为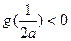
又
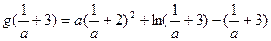
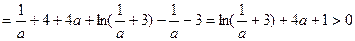
∴
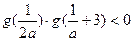 ∴方程
∴方程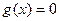 恰好有一解 -------11分
恰好有一解 -------11分(2)当
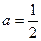 时,
时,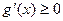 ,
,∴函数
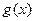 为增函数,由(1)得方程
为增函数,由(1)得方程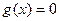 也恰好有一解 -------12分
也恰好有一解 -------12分(3)当
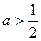 时,
时,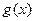 的单调增区间为
的单调增区间为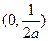 ,
,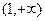 ,单调减区间为
,单调减区间为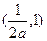
同(1)可得方程
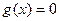 在
在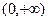 至少有一解
至少有一解综上所述所求的
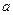 取值范围为
取值范围为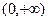 -------14分
-------14分 | ||||
| ||||

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

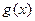 的单调递增区间;
的单调递增区间;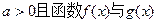 的图像有公共点,且在该点处的切线相同,用a表示b,并求b的最大值。
的图像有公共点,且在该点处的切线相同,用a表示b,并求b的最大值。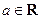 ,函数
,函数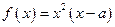 .
.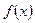 在区间
在区间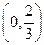 内是减函数,求实数
内是减函数,求实数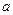 的取值范围;
的取值范围;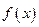 在区间
在区间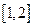 上的最小值
上的最小值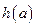 ;
;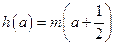 有两个不相等的实数解,求实数
有两个不相等的实数解,求实数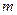 的取值范围.
的取值范围.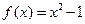 与函数
与函数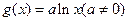 .
.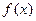 ,
,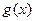 的图像在点
的图像在点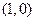 处有公共的切线,求实数
处有公共的切线,求实数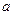 的值;
的值;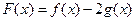 ,求函数
,求函数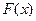 的值.
的值.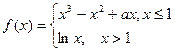 ,在x=1处连续.
,在x=1处连续.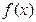 的单调减区间;
的单调减区间;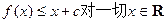 恒成立,求c的取值范围.
恒成立,求c的取值范围.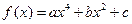 的图象过点
的图象过点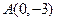 ,且它在
,且它在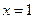 处的切线方程为
处的切线方程为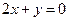 .
.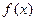 的解析式;
的解析式;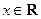 ,不等式
,不等式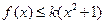 恒成立,求实数
恒成立,求实数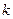 的取值范围.
的取值范围.



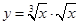 的导数
的导数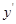 为( ).
为( ).



 是
是 的导函数,则
的导函数,则 的值是 .
的值是 .