Question

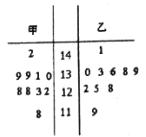
【题目】为了解甲、乙两个班级某次考试的数学成绩（单位：分），从甲、乙两个班级中分别随机抽取5名学生的成绩作样本，如图是样本的茎叶图，规定：成绩不低于120分时为优秀成绩．

（1）从甲班的样本中有放回的随机抽取2个数据，求其中只有一个优秀成绩的概率；
（2）从甲、乙两个班级的样本中分别抽取2名学生的成绩，记获优秀成绩的总人数为X，求X的分布列．

Answer 1

【答案】
（1）解：由茎叶图知甲班样本的5个数据中优秀成绩有2个，非优秀成绩有3个，

从甲班的样本中有放回的随机抽取2个数据，

基本事件总数n=5×5=25，

其中只有一个优秀成绩包含的基本事件个数为：

m=2×5+5×2=20，

∴其中只有一个优秀成绩的概率p= = =

（2）解：由茎叶图知甲班样本的5个数据中优秀成绩有2个，非优秀成绩有3个，

乙班样本的5个数据中优秀成绩有1个，非优秀成绩有4个，

∴X的可能取值为0，1，2，3，

P（X=0）= = ，

P（X=1）= = ，

P（X=2）= = ，

P（X=3）= = ，

∴X的分布列为：

X	0	1	2	3
P

【解析】（1）由茎叶图知甲班样本的5个数据中优秀成绩有2个，非优秀成绩有3个，由此能求出从甲班的样本中有放回的随机抽取2个数据，其中只有一个优秀成绩的概率．（2）由茎叶图知甲班样本的5个数据中优秀成绩有2个，非优秀成绩有3个，乙班样本的5个数据中优秀成绩有1个，非优秀成绩有4个，X的可能取值为0，1，2，3，分别求出相应的概率，由此能求出X的分布列．