题目内容
【题目】边长为![]() 的菱形
的菱形![]() ,其顶角
,其顶角![]() 为
为![]() .用 分别
.用 分别![]() 平行的三组等距平行线,将菱形划分成
平行的三组等距平行线,将菱形划分成![]() 个边长为1的正三角形.试求以图中的线段为边的梯形个数
个边长为1的正三角形.试求以图中的线段为边的梯形个数![]() .
.
【答案】![]()
【解析】
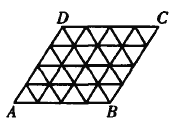
由于图中任两条线段所在的直线,或者平 行或者相交成60°的锐角,
因此,由图中线段组成的所有梯形都是底角为60°的等腰梯形.对于这种梯形,
若两腰延长线的交点在菱形内部或周界上,则称为“内置梯形”;若交点在菱形外,则称为“外延梯形”.
(1)先求内置梯形的个数![]() .
.
将边长为![]() 的正三角形称为“
的正三角形称为“![]() 级三角形”,相应地,下底(较长底边)的长为
级三角形”,相应地,下底(较长底边)的长为![]() 的梯形称为“
的梯形称为“![]() 级梯形”,
级梯形”,
再将腰长为![]() 的
的![]() 级梯形称为“
级梯形称为“![]() 梯 形”.
梯 形”.
图中所有正三角形,要么顶点朝上,要么顶点朝下,分别称作“顺置三角形”与“倒置三角形”.
易见,每个![]() 梯形,可看作是由一个
梯形,可看作是由一个![]() 级三角形切去一个
级三角形切去一个![]() 级三角形而得到的.
级三角形而得到的.
每个![]() 级三角形所切出的
级三角形所切出的![]() 级梯形有
级梯形有![]() 种情况(其中,
种情况(其中,![]() 梯形各3个).
梯形各3个).
现计算图中![]() 级三角形的个数:取
级三角形的个数:取![]() 为原点并以
为原点并以![]() 为
为![]() 轴、
轴、![]() 轴建立斜角坐标系,每个
轴建立斜角坐标系,每个![]() 级顺置三角形,下底左端点
级顺置三角形,下底左端点![]() 的横坐标可取
的横坐标可取![]() 共
共![]() 个值,纵坐标也可取
个值,纵坐标也可取![]() 共
共![]() 个值.因此,
个值.因此,![]() 级顺置三角形有
级顺置三角形有![]() 个.据对称性,
个.据对称性, ![]() 级倒置三角形也有
级倒置三角形也有![]() 个.从而,
个.从而, ![]() 级三角形有
级三角形有![]() 个.于是,
个.于是, ![]() 级内置梯形有
级内置梯形有![]() 个.
个.
求和得
![]()
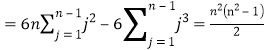
(2)再求外延梯形的个数![]() .
.
先考虑外延交点在线段AB外侧的情况.如图 10,任取![]() ,使
,使![]() ,设诸点的斜角坐标为:
,设诸点的斜角坐标为:![]() ,
,![]() ,
,![]() ,
,![]() .延长
.延长![]() ,交直线
,交直线![]() 于点
于点![]() ,位于
,位于![]() 延长线上的交点共有
延长线上的交点共有![]() 个.对于确定的
个.对于确定的![]() ,
,![]() 为一个倒置正三角形,当点
为一个倒置正三角形,当点![]() 在
在![]() 上移动时,点
上移动时,点![]() 在直线
在直线![]() 上移动,由于
上移动,由于![]()
![]() ,
,
这两条线段间的平行线共有![]() 条(包括这两条线在内),任两条这种平行线都在
条(包括这两条线在内),任两条这种平行线都在![]() 截出一个梯形.因此,这种梯形共有
截出一个梯形.因此,这种梯形共有![]() 个,它们都以
个,它们都以![]() 为外延交点.而
为外延交点.而![]() 延长线位于
延长线位于![]() 外侧的交点
外侧的交点![]() 共有
共有![]() 个,故当
个,故当![]() 固定时,共得到
固定时,共得到![]() 个外延梯形.现让
个外延梯形.现让![]() 取遍
取遍![]() ,因此,位于
,因此,位于![]() 外侧的全部外延
外侧的全部外延![]() 点共形成
点共形成![]() 个外延梯形.
个外延梯形.
据对称性,在菱形另三条边外侧的外延点,也分别形成同样数目的外延梯形,从而,全部外延梯形的个数为
![]()
![]()
![]()
故![]()

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生.新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
(1)根据上表说明,能否有99%把握认为愿意参加新生接待工作与性别有关;
(2)现从参与问卷调查且愿意参加新生接待工作的学生中,采用按性别分层抽样的方法,选取10人.若从这10人中随机选取3人到火车站迎接新生,设选取的3人中女生人数为![]() ,写出
,写出![]() 的分布列,并求
的分布列,并求![]() .
.
附: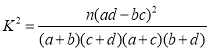 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |