题目内容
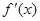 是函数
是函数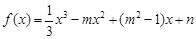 的导函数,若函数
的导函数,若函数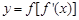 在区间
在区间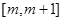 上单调递减,则实数
上单调递减,则实数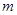 的取值范围是( )
的取值范围是( )A.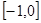 | B.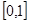 | C.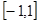 | D.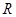 |
A
解:因为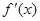 是函数
是函数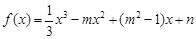 的导函数,函数
的导函数,函数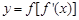 在区间
在区间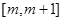 上单调递减,即
上单调递减,即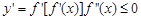 在给定的区间上恒成立。利用分离参数的思想得到m的取值范围为
在给定的区间上恒成立。利用分离参数的思想得到m的取值范围为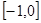
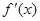 是函数
是函数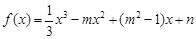 的导函数,函数
的导函数,函数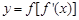 在区间
在区间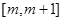 上单调递减,即
上单调递减,即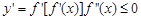 在给定的区间上恒成立。利用分离参数的思想得到m的取值范围为
在给定的区间上恒成立。利用分离参数的思想得到m的取值范围为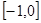

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
题目内容
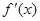 是函数
是函数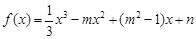 的导函数,若函数
的导函数,若函数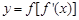 在区间
在区间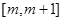 上单调递减,则实数
上单调递减,则实数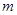 的取值范围是( )
的取值范围是( )A.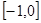 | B.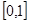 | C.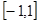 | D.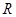 |
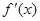 是函数
是函数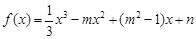 的导函数,函数
的导函数,函数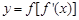 在区间
在区间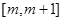 上单调递减,即
上单调递减,即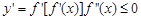 在给定的区间上恒成立。利用分离参数的思想得到m的取值范围为
在给定的区间上恒成立。利用分离参数的思想得到m的取值范围为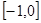

 小学课时特训系列答案
小学课时特训系列答案