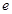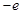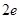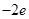题目内容
如图所示,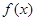 是定义在区间
是定义在区间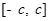 (
(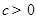 )上的奇函数,令
)上的奇函数,令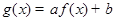 ,并有关于函数
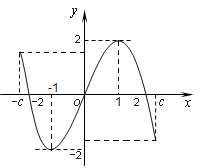
,并有关于函数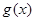 的四个论断:
的四个论断:
①若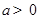 ,对于
,对于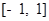 内的任意实数
内的任意实数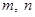 (
(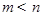 ),
),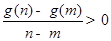 恒成立;
恒成立;
②函数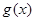 是奇函数的充要条件是
是奇函数的充要条件是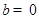 ;
;
③若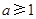 ,
,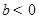 ,则方程
,则方程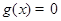 必有3个实数根;
必有3个实数根;
④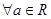 ,
,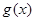 的导函数
的导函数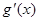 有两个零点;
有两个零点;
其中所有正确结论的序号是( ).
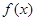 是定义在区间
是定义在区间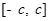 (
(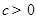 )上的奇函数,令
)上的奇函数,令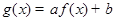 ,并有关于函数
,并有关于函数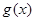 的四个论断:
的四个论断:
①若
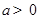 ,对于
,对于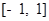 内的任意实数
内的任意实数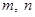 (
(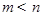 ),
),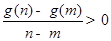 恒成立;
恒成立;②函数
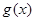 是奇函数的充要条件是
是奇函数的充要条件是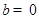 ;
;③若
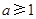 ,
,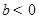 ,则方程
,则方程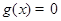 必有3个实数根;
必有3个实数根;④
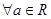 ,
,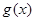 的导函数
的导函数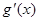 有两个零点;
有两个零点; 其中所有正确结论的序号是( ).
| A.①② | B.①②③ |
| C.①④ | D.②③④ |
A
①因为f(x)在[-1,1]上是增函数,当a>0时,g(x) 在[-1,1]上也是增函数.正确;
②若g(x)为奇函数,则g(-x)+g(x)=0恒成立,所以2b=0,b=0.正确。
③y=af(x)的图像,与直线y=-b不一定有三个交点,因而错。
④当a=0时,g(x)=b,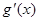 =0有无数个零点。错。
=0有无数个零点。错。
②若g(x)为奇函数,则g(-x)+g(x)=0恒成立,所以2b=0,b=0.正确。
③y=af(x)的图像,与直线y=-b不一定有三个交点,因而错。
④当a=0时,g(x)=b,
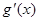 =0有无数个零点。错。
=0有无数个零点。错。
练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
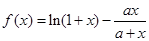 在
在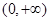 上单调递增,求实数
上单调递增,求实数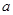 的取值范围.
的取值范围.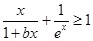 在
在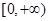 上恒成立,求实数
上恒成立,求实数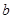 的最大值.
的最大值.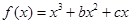 的导函数的图象关于直线x=2对称.
的导函数的图象关于直线x=2对称.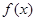 在
在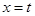 处取得极小值,记此极小值为
处取得极小值,记此极小值为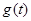 ,求
,求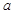 为正实数,
为正实数,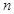 为自然数,抛物线
为自然数,抛物线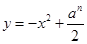 与
与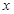 轴正半轴相交于点
轴正半轴相交于点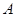 ,设
,设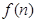 为该抛物线在点
为该抛物线在点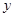 轴上的截距。
轴上的截距。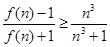 成立的
成立的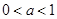 时,比较
时,比较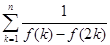 与
与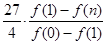 的大小,并说明理由。
的大小,并说明理由。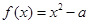 .
.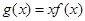 在区间
在区间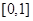 的最小值;
的最小值;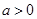 时,记曲线
时,记曲线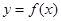 在
在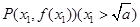 处的切线为
处的切线为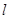 ,
,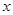 轴交于点
轴交于点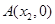 ,求证:
,求证: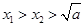 .
.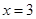 是函数
是函数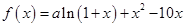 的一个极值点.
的一个极值点.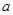 ;
;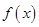 的单调区间;
的单调区间;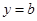 与函数
与函数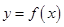 的图象有3个交点,求
的图象有3个交点,求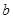 的取值范围.
的取值范围.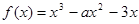 ,
,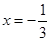 是
是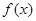 的极值点,求
的极值点,求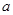 值;
值;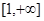 上是增函数,求实数
上是增函数,求实数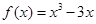 ,(1)求函数
,(1)求函数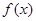 极值.(2)求函数
极值.(2)求函数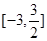 上的最大值和最小值.
上的最大值和最小值.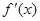 是函数
是函数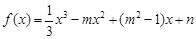 的导函数,若函数
的导函数,若函数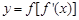 在区间
在区间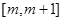 上单调递减,则实数
上单调递减,则实数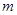 的取值范围是( )
的取值范围是( )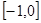
 ,则
,则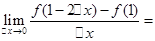 ( )
( )