题目内容
【题目】如图，设抛物线y2=2px（p＞0）的焦点为F，抛物线上的点A到y轴的距离等于|AF|﹣1，
（1）求p的值；
（2）若直线AF交抛物线于另一点B，过B与x轴平行的直线和过F与AB垂直的直线交于点N，AN与x轴交于点M，求M的横坐标的取值范围．
【答案】
（1）
解：由题意可得，抛物线上点A到焦点F的距离等于A到直线x=﹣1的距离，
由抛物线定义得， 
，即p=2
（2）
解：由（1）得，抛物线方程为y2=4x，F（1，0），可设（t2，2t），t≠0，t≠±1，
∵AF不垂直y轴，
∴设直线AF：x=sy+1（s≠0），
联立 
，得y2﹣4sy﹣4=0．
y1y2=﹣4，
∴B 
，
又直线AB的斜率为 
，故直线FN的斜率为 
，
从而得FN： 
，直线BN：y=﹣ 
，
则N（ 
），
设M（m，0），由A、M、N三点共线，得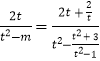 
，
于是m= 
= 
，得m＜0或m＞2．
经检验，m＜0或m＞2满足题意．
∴点M的横坐标的取值范围为（﹣∞，0）∪（2，+∞）．
【解析】（1）利用抛物线的性质和已知条件求出抛物线方程，进一步求得p值；
（2）设出直线AF的方程，与抛物线联立，求出B的坐标，求出直线AB，FN的斜率，从而求出直线BN的方程，根据A、M、N三点共线，可求出M的横坐标的表达式，从而求出m的取值范围．
本题考查抛物线的简单性质，考查直线与圆锥曲线位置关系的应用，考查数学转化思想方法，属中档题．
练习册系列答案
相关题目
