题目内容
【题目】如图,三棱柱ABC﹣A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,A1A=AB=6,D为AC中点.

(1)求三棱锥C1﹣BCD的体积;
(2)求证:平面BC1D⊥平面ACC1A1;
(3)求证:直线AB1∥平面BC1D.
【答案】(1)![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
(1)先根据△ABC为正三角形,D为AC中点,得到BD⊥AC,求出△BCD的面积;再根据C1C⊥底面ABC,根据体积公式求出三棱锥C1-BCD的体积;
(2)先根据A1A⊥底面ABC,得到A1A⊥BD,再结合BD⊥AC即可得到BD⊥平面ACC1A1.即可证平面BC1D⊥平面ACC1A1;
(3)连接B1C交BC1于O,连接OD,根据D为AC中点,O为B1C中点可得OD∥AB1,即可证:直线AB1∥平面BC1D.
(1)∵△ABC为正三角形,D为AC中点,∴BD⊥AC,
由AB=6可知,CD=3,BD=![]() ,∴S△BCD=
,∴S△BCD=![]() CDBD=
CDBD=![]() .
.
又∵A1A⊥底面ABC,且A1A=AB=6,∴C1C⊥底面ABC,且C1C=6,
∴VC1BCD=![]() S△BCDC1C=
S△BCDC1C=![]()
(2)∵A1A⊥底面ABC,∴A1A⊥BD.
又BD⊥AC,∴BD⊥平面ACC1A1.
又BD平面BC1D,∴平面BC1D⊥平面ACC1A1.
(3)连接B1C交BC1于O,连接OD,
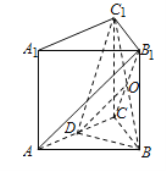
在△B1AC中,D为AC中点,O为B1C中点,所以OD∥AB1,
又OD平面BC1D,∴直线AB1∥平面BC1D.

 阅读快车系列答案
阅读快车系列答案【题目】某车间为了规定工时定额,需确定加工零件所花费的时间,为此做了4次试验,得到的数据如下:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 4.5 |
若加工时间![]() 与零件个数
与零件个数![]() 之间有较好的相关关系.
之间有较好的相关关系.
(1)求加工时间与零件个数的线性回归方程![]() .
.
(2)试预报加工10个零件需要的时间.
附录:参考公式: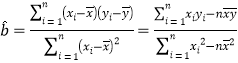 ,
,![]() .
.

