题目内容
【题目】
下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图
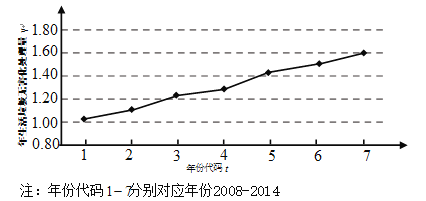
（1）由折线图看出，可用线性回归模型拟合
与
的关系，请建立
关于
的回归方程（系数精确到0.01）；
（2）预测2018年我国生活垃圾无害化处理量.
附注：
参考公式：设具有线性相关关系的两个变量
的一组观察值为
，
则回归直线方程
的系数为：
， 
.
参考数据: 
， 
.
【答案】(1) 
(2)2.02
【解析】试题分析： 
由折线图看出， 
与
之间存在较强的正相关关系，将已知数据代入相关系数方程，根据已知中的数据，求出回归系数，可得回归方程，
将
年对应的
11，代入回归方程，即可得到答案；
解析：（1）由折线图中数据和附注中参考数据得
，
，
因此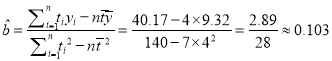
又由
得
.
所以，
关于
的回归方程为： 
.
注意：为使系数
精确到0.01的值更精准，前面
和
小数点后应保留3位参与运算.
（2）将2018年对应的
代入回归方程得： 
.
所以预测2018年我国生活垃圾无害化处理量将约2.02亿吨.
练习册系列答案
相关题目
【题目】探究函数
的最小值，并确定取得最小值时x的值.列表如下：
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 4.8 | 7.57 | … |
请观察表中y值随x值变化的特点，完成以下的问题.
函数
在区间（0，2）上递减；
函数
在区间 上递增.
当
时， 
.
证明：函数
在区间（0，2）递减.
思考：函数
时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）
