Question

9．如图，抛物线C₁：y²=2px与椭圆C₂：$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1在第一象限的交点为B，O为坐标原点，A为椭圆的右顶点，△OAB的面积为$\frac{8\sqrt{6}}{3}$．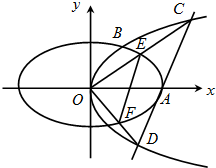
（Ⅰ）求抛物线C₁的方程；
（Ⅱ）过A点作直线l交C₁于C、D 两点，射线OC、OD分别交C₂于E、F两点，记△OEF和△OCD的面积分别为S₁和S₂，问是否存在直线l，使得S₁：S₂=3：77？若存在，求出直线l的方程；若不存在，请说明理由．

Answer 1

分析 （Ⅰ）通过三角形△OAB的面积，求出B的纵坐标，然后求出横坐标，代入抛物线的方程，求出p，即可得到抛物线方程．
（Ⅱ） 存在直线l：x±11y-4=0符合条件．通过设直线l的方程x=my+4，与抛物线联立，设C（x₁，y₁），D（x₂，y₂），通过$\frac{{S}_{2}}{{S}_{1}}=\frac{|{y}_{1}||{y}_{2}|}{|{y}_{E}||{y}_{F}|}$，求出${y_E}^2•$${y_F}^2=\frac{36×256}{{121+48{m^2}}}$，然后求出m，得到直线l即可．

解答 解：（Ⅰ）因为△OAB的面积为$\frac{{8\sqrt{6}}}{3}$，所以${y_B}=\frac{{4\sqrt{6}}}{3}$，…（2分）
代入椭圆方程得$B（\frac{4}{3}，\frac{{4\sqrt{6}}}{3}）$，
抛物线的方程是：y²=8x…（4分）
（Ⅱ） 存在直线l：x±11y-4=0符合条件
解：显然直线l不垂直于y轴，故直线l的方程可设为x=my+4，
与y²=8x联立得y²-8my-32=0．
设C（x₁，y₁），D（x₂，y₂），则y₁+y₂=8m，y₁•y₂=-32
∴$\frac{S_2}{S_1}=\frac{{\frac{1}{2}|{OC}||{OD}|sin∠COD}}{{\frac{1}{2}|{OE}||{OF}|sin∠EOF}}=\frac{{|{OC}||{OD}|}}{{|{OE}||{OF}|}}=\frac{{|{y_1}||{y_2}|}}{{|{y_E}||{y_F}|}}$=$\frac{32}{{|{{y_E}{y_F}}|}}$．…（6分）
由直线OC的斜率为$\frac{y_1}{x_1}=\frac{8}{y_1}$，故直线OC的方程为$y=\frac{8}{y_1}x$，与$\frac{x^2}{16}+\frac{y^2}{12}=1$联立得${y_E}^2（\frac{{{y_1}^2}}{64•16}+\frac{1}{12}）=1$，同理${y_F}^2（\frac{{{y_2}^2}}{64•16}+\frac{1}{12}）=1$，
所以${y_E}^2•$${y_F}^2（\frac{{{y_1}^2}}{64•16}+\frac{1}{12}）（\frac{{{y_2}^2}}{64•16}+\frac{1}{12}）=1$…（8分）
可得${y_E}^2•$${y_F}^2=\frac{36×256}{{121+48{m^2}}}$
要使$\frac{S_2}{S_1}=\frac{77}{3}$，只需$\frac{{{{32}^2}（121+48{m^2}）}}{36×256}={（{\frac{77}{3}}）^2}$…（10分）
即121+48m²=49×121
解得m=±11，
所以存在直线l：x±11y-4=0符合条件…（12分）

点评 本题考查圆锥曲线方程的综合应用，考查分析问题以及转化思想的应用，考查计算能力．