题目内容
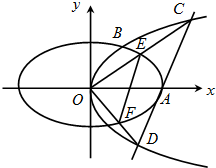
2．
如图，已知椭圆M：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），其离心率为$\frac{\sqrt{3}}{2}$，两条准线之间的距离为$\frac{8\sqrt{3}}{3}$．B，C分别为椭圆M的上、下顶点，过点T（t，2）（t≠0）的直线TB，TC分别与椭圆M交于E，F两点．（1）求椭圆M的标准方程；
（2）若△TBC的面积是△TEF的面积的k倍，求k的最大值．
分析 （1）由椭圆的离心率公式和准线方程，结合椭圆的a，b，c的关系，计算即可得到；
（2）分别求出直线PB，TC的方程，代入椭圆方程，求得交点E，F的横坐标，再由三角形的面积公式，结合二次函数，计算即可得到最大值．
解答 解：（1）由题意得e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$，$\frac{2{a}^{2}}{c}$=$\frac{8\sqrt{3}}{3}$，
解得a=2，c=$\sqrt{3}$，b=1，
则椭圆方程为$\frac{{x}^{2}}{4}$+y2=1；
（2）由B（0，1），C（0，-1），T（t，2），
则直线TB：y=$\frac{1}{t}$x+1，代入椭圆方程可得，（1+$\frac{4}{{t}^{2}}$）x2+$\frac{8}{t}$x=0，
解得xE=$\frac{-8t}{4+{t}^{2}}$，
直线TC：y=$\frac{3}{t}$x-1，代入椭圆方程可得xF=$\frac{24t}{36+{t}^{2}}$，
k=$\frac{{S}_{△TBC}}{{S}_{△TEF}}$=$\frac{\frac{1}{2}TB•TC•sin∠BTC}{\frac{1}{2}TE•TF•sin∠ETF}$=$\frac{TB•TC}{TE•TF}$=$\frac{{x}_{T}-{x}_{B}}{{x}_{T}-{x}_{E}}$•$\frac{{x}_{T}-{x}_{C}}{{x}_{T}-{x}_{F}}$=$\frac{t}{t+\frac{8t}{4+{t}^{2}}}$•$\frac{t}{1-\frac{24t}{36+{t}^{2}}}$
=$\frac{（{t}^{2}+4）（{t}^{2}+36）}{（{t}^{2}+12）（{t}^{2}+12）}$，
令t2+12=m＞12，则k=$\frac{（m-8）（m+24）}{{m}^{2}}$=1+$\frac{16}{m}$-$\frac{192}{{m}^{2}}$≤$\frac{4}{3}$，
当且仅当m=24，即t=±2$\sqrt{3}$时，取得“=”，
所以k的最大值为$\frac{4}{3}$．
点评 本题考查椭圆的方程和性质，主要考查椭圆的离心率和方程的运用，联立直线方程和椭圆方程，求得交点，同时考查三角形的面积公式的运用，考查运算能力，属于中档题．
在△AOB中，已知∠AOB=$\frac{π}{2}$，∠BAO=$\frac{π}{6}$，AB=4，D为线段AB的中点，△AOC是由△AOB绕直线AO旋转而成，记二面角B-AO-C的大小为θ．（1）有一个面是边长为1的等边三角形；
（2）有两个面是等腰直角三角形．
那么四面体A-BCD的体积的取值集合是（ ）
| A． | $\{\frac{1}{2}，\frac{{\sqrt{2}}}{12}\}$ | B． | $\{\frac{1}{6}，\frac{{\sqrt{3}}}{12}\}$ | C． | $\{\frac{{\sqrt{2}}}{12}，\frac{{\sqrt{3}}}{12}，\frac{{\sqrt{2}}}{24}\}$ | D． | $\{\frac{1}{6}，\frac{{\sqrt{2}}}{12}，\frac{{\sqrt{2}}}{24}\}$ |
如图，正方形ABCD与ABEF构成一个60°的二面角，将△ACD绕AD旋转一周，则在旋转过程中，直线AC与平面ABEF所成角的取值范围是[15°，75°]．