题目内容
19.写出下列数列的一个通项公式.(1)1,-2,3,-4,5,…;
(2)7,77,777,7777,…;
(3)1$\frac{1}{2}$,3$\frac{1}{4}$,5$\frac{1}{8}$,7$\frac{1}{16}$,…;
(4)$\frac{{2}^{2}-1}{2}$,$\frac{{3}^{2}-1}{3}$,$\frac{{4}^{2}-1}{4}$,$\frac{{5}^{2}-1}{5}$,…;
(5)-$\frac{1}{1×2}$,$\frac{1}{2×3}$,-$\frac{1}{3×4}$,$\frac{1}{4×5}$,….
分析 (1)分符号、绝对值可得${a}_{n}=(-1)^{n}n$;
(2)由于9,99,999,9999,…,其通项公式为${a}_{n}=1{0}^{n}-1$,即可得出7,77,777,7777,…其通项公式为:bn=$\frac{7}{9}(1{0}^{n}-1)$;
(3)把每一项分开可得:其通项公式为:an=(2n-1)+$\frac{1}{{2}^{4}}$;
(4)观察其分母为n+1,分子为(n+1)2-1,可得其通项公式为:an=$\frac{(n+1)^{2}-1}{n+1}$;
(5)分符号与分母可得:其通项公式为:$(-1)^{n}\frac{1}{n(n+1)}$.
解答 解:(1)1,-2,3,-4,5,…,可得${a}_{n}=(-1)^{n}n$;
(2)∵9,99,999,9999,…,其通项公式为${a}_{n}=1{0}^{n}-1$,∴7,77,777,7777,…其通项公式为:bn=$\frac{7}{9}(1{0}^{n}-1)$;
(3)1$\frac{1}{2}$,3$\frac{1}{4}$,5$\frac{1}{8}$,7$\frac{1}{16}$,…,其通项公式为:an=(2n-1)+$\frac{1}{{2}^{4}}$;
(4)$\frac{{2}^{2}-1}{2}$,$\frac{{3}^{2}-1}{3}$,$\frac{{4}^{2}-1}{4}$,$\frac{{5}^{2}-1}{5}$,…,其通项公式为:an=$\frac{(n+1)^{2}-1}{n+1}$;
(5)-$\frac{1}{1×2}$,$\frac{1}{2×3}$,-$\frac{1}{3×4}$,$\frac{1}{4×5}$,…,其通项公式为:$(-1)^{n}\frac{1}{n(n+1)}$.
点评 本题考查了通过观察分析猜想归纳求数列的通项公式的方法,考查了推理能力与计算能力,属于基础题.

 阅读快车系列答案
阅读快车系列答案| A. | (-3,0)∪(3,4] | B. | (-4,-3)∪(1,2)∪(2,3) | C. | (-1,0)∪(1,2)∪(2,3) | D. | (-4,-3)∪(-1,0)∪(1,3) |
| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
| A. | {2} | B. | {-1} | C. | {$\frac{1}{2}$} | D. | {-1,2} |
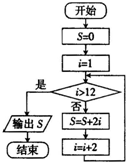
| A. | 25 | B. | 55 | C. | 72 | D. | 110 |