题目内容
19．曲线y=2x-x3在点（1，1）处的切线方程为x+y-2=0．分析 根据导数的几何意义求出函数在x=1处的导数，从而得到切线的斜率，再利用点斜式方程写出切线方程即可．
解答 解：y=2x-x3的导数为y'=2-3x2
即有在点（1，1）处的切线斜率为k=y'|x=1=-1，
而切点的坐标为（1，1），
∴曲线y=2x-x3在x=1的处的切线方程为y-1=-（x-1），
即为x+y-2=0．
故答案为：x+y-2=0．
点评 本题主要考查了利用导数研究曲线上某点切线方程，考查运算求解能力，属于基础题．
练习册系列答案
状元及第系列答案
同步奥数系列答案
相关题目
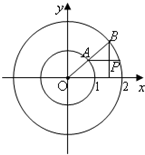如图所示，射线OA与单位圆交于A，与圆x2+y2=4交于点B，过A平行于x轴的直线与过B与x轴垂直的直线交于P点，OA与x轴的夹角为x，若f（x）=$\overrightarrow{OA}$•$\overrightarrow{OP}$+cosx（cosx+2$\sqrt{3}$sinx）
7．已知集合A={x|x2=2}，B={1，$\sqrt{2}$，2}，则A∩B=（ ）
| A． | {$\sqrt{2}$} | B． | {2} | C． | {-$\sqrt{2}$，1，$\sqrt{2}$，2} | D． | {-2，1，$\sqrt{2}$，2} |
11．
如图，一隧道截面由一个长方形和抛物线构成，现欲在隧道抛物线拱顶上安装交通信息采集装置，若位置C对隧道底AB的张角θ最大时采集效果最好，则采集效果最好时位置C到AB的距离是（ ）
如图，一隧道截面由一个长方形和抛物线构成，现欲在隧道抛物线拱顶上安装交通信息采集装置，若位置C对隧道底AB的张角θ最大时采集效果最好，则采集效果最好时位置C到AB的距离是（ ）| A． | 2$\sqrt{2}$m | B． | 2$\sqrt{3}$m | C． | 4m | D． | 6m |