题目内容
20.函数f(x)=ln($\frac{1}{x}$+1)(x>0)的反函数f-1(x)=$\frac{1}{{e}^{x}-1}$,x∈(0,+∞).分析 直接利用反函数的求法求解即可.
解答 解:函数f(x)=ln($\frac{1}{x}$+1)(x>0),f(x)∈(0,+∞).
$\frac{1}{x}$+1=ey,解得x=$\frac{1}{{e}^{y}-1}$,
函数f(x)=ln($\frac{1}{x}$+1)(x>0)的反函数f-1(x)=$\frac{1}{{e}^{x}-1}$,x∈(0,+∞).
故答案为:$\frac{1}{{e}^{x}-1}$,x∈(0,+∞).
点评 本题考查反函数与原函数的关系,考查计算能力.注意函数的定义域.

练习册系列答案
相关题目
15.已知函数f(x)=3x(x∈R)的反函数为g(x),则g($\frac{1}{2}$)=( )
| A. | -log32 | B. | log32 | C. | -log23 | D. | log23 |
5.设m,n是两条不同的直线,α,β是两个不同的平面,则( )
| A. | 若m∥α,m∥β,则α∥β | B. | 若m∥α,m∥n,则n∥α | C. | 若m⊥α,m∥β,则α⊥β | D. | 若m∥α,n?α,则m∥n |
 ,
, 满足不等式组
满足不等式组 时,
时, 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.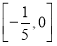
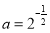 ,
, ,
,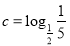 ,则( )
,则( ) B.
B.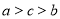
 D.
D.