题目内容
一个圆柱底面直径与高相等,其体积与一个球的体积之比是3:2,则这个圆柱的表面积与这个球的表面积之比为( )
( )1:1 (
)1:1 (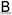 ) 1:
) 1: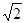 (
(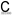 )
) 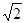 :
: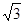 (
(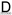 ) 3:2
) 3:2
(
 )1:1 (
)1:1 ( ) 1:
) 1: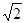 (
(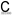 )
) 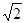 :
: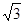 (
( ) 3:2
) 3:2D
考点:
分析:根据圆柱体积与球的体积之比是3:2,确定其半径之比,进而可得圆柱的表面积与球的表面积之比.
解答:解:设圆柱底面直径为2R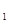 ,球的半径为R
,球的半径为R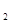 ,则圆柱的体积为2πR
,则圆柱的体积为2πR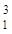 ,球的体积为
,球的体积为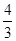 πR
πR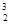
∵圆柱体积与球的体积之比是3:2
∴2πR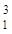 :
: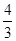 πR
πR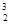 =3:2
=3:2
∴R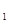 :R
:R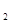 =1:1
=1:1
∵圆柱的表面积为2πR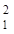 + 4πR
+ 4πR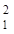 =6πR
=6πR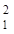 ,球的表面积4πR
,球的表面积4πR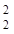
∴圆柱的表面积与球的表面积之比为6πR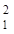 :4πR
:4πR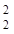 =3:2
=3:2
故选D.
点评:本题考查圆柱与球的体积与表面积的计算,正确运用公式是关键,属于基础题.
分析:根据圆柱体积与球的体积之比是3:2,确定其半径之比,进而可得圆柱的表面积与球的表面积之比.
解答:解:设圆柱底面直径为2R
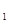 ,球的半径为R
,球的半径为R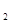 ,则圆柱的体积为2πR
,则圆柱的体积为2πR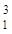 ,球的体积为
,球的体积为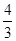 πR
πR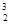
∵圆柱体积与球的体积之比是3:2
∴2πR
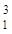 :
: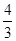 πR
πR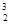 =3:2
=3:2∴R
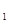 :R
:R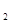 =1:1
=1:1∵圆柱的表面积为2πR
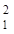 + 4πR
+ 4πR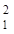 =6πR
=6πR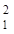 ,球的表面积4πR
,球的表面积4πR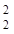
∴圆柱的表面积与球的表面积之比为6πR
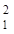 :4πR
:4πR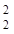 =3:2
=3:2故选D.
点评:本题考查圆柱与球的体积与表面积的计算,正确运用公式是关键,属于基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目

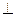 面ABCD,E为AB中点,求二面角E-SC-D的大小;
面ABCD,E为AB中点,求二面角E-SC-D的大小; EC的距离。
EC的距离。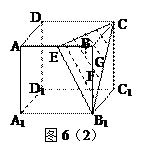
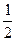 B.
B.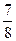 C.
C.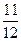 D.
D.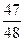
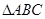 的三边分别为
的三边分别为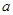 ,
,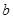 ,
,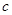 ,
,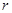 ,则
,则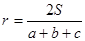 ,类比这个结论可知:四面体
,类比这个结论可知:四面体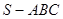 的四个面面积分别为
的四个面面积分别为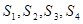 ,内切球半径为
,内切球半径为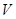 ,则
,则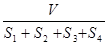
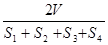
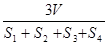
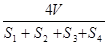
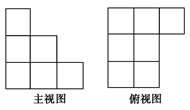
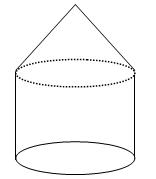
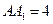 ,若侧面
,若侧面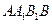 水平放置时,液面恰好过
水平放置时,液面恰好过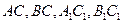 的中点,当底面
的中点,当底面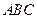 水平放
水平放 置时,液面的高为
置时,液面的高为 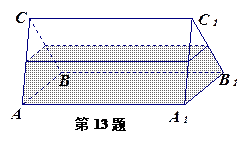
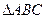 的三个顶点距离均为1cm的平面共有 .
的三个顶点距离均为1cm的平面共有 .