题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且短轴长为2.
,且短轴长为2.
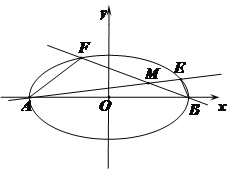
(1)求椭圆的标准方程;
(2)已知![]() 分别为椭圆的左右顶点,
分别为椭圆的左右顶点, ![]() ,
,![]() ,且
,且![]() ,直线
,直线![]() 与
与![]() 分别与椭圆交于
分别与椭圆交于![]() 两点,
两点,
(i)用![]() 表示点
表示点![]() 的纵坐标;
的纵坐标;
(ii)若![]() 面积是
面积是![]() 面积的5倍,求
面积的5倍,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由b=2, ![]() ,可求得标准方程。(2)设直线方程与椭圆方程组方程组,可解得交点坐标E,F。三角形面积公式用
,可求得标准方程。(2)设直线方程与椭圆方程组方程组,可解得交点坐标E,F。三角形面积公式用![]() ,面积比转化为线段比,再转化为y坐标的比。
,面积比转化为线段比,再转化为y坐标的比。
试题解析:(1)由题意知 ,解得
,解得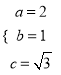 ,
,
椭圆的标准方程为: ![]() .
.
(2)(i) ![]()
![]() ,
, ![]() ,
, ![]() ,且
,且 ![]() ,
,
![]() 直线
直线 ![]() 的斜率为
的斜率为 ![]() ,直线
,直线 ![]() 的斜率为
的斜率为 ![]() ,
,
![]() 直线
直线 ![]() 的方程为
的方程为 ![]() ,直线
,直线 ![]() 的方程为
的方程为 ![]() ,
,
由 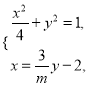 得
得 ![]() ,
,
点E的纵坐标 ![]() ,
,
由 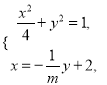 得
得 ![]() ,
,
![]() ,
,
(ii)![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
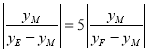 ,即
,即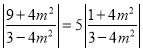 ,解得
,解得![]()

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
【题目】“双十一”期间,某淘宝店主对其商品的上架时间![]() (小时)和销售量
(小时)和销售量![]() (件)的关系作了统计,得到了如下数据并研究.
(件)的关系作了统计,得到了如下数据并研究.
上架时间 | 2 | 4 | 6 | 8 | 10 | 12 |
销售量 | 64 | 138 | 205 | 285 | 360 | 430 |
(1)求表中销售量![]() 的平均数和中位数;
的平均数和中位数;
(2)① 作出散点图,并判断变量![]() 与
与![]() 是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程
是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程![]() ;
;
②若根据①中线性回归方程得到商品上架12小时的销售量的预测值与检测值不超过3件,则认为得到的线性回归方程是理想的,试问:①中的线性回归方程是否理想.
附:线性回归方程![]() 中,
中, 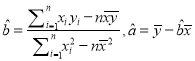 .
.