题目内容
【题目】已知数列![]() 的各项均为正数,前
的各项均为正数,前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)设![]() ,求
,求![]() .
.
【答案】(1)证明见解析;(2) ![]()
【解析】试题分析:(1)利用an=![]() 即a1=1,当n≥2时,得2
即a1=1,当n≥2时,得2![]() =
=![]() +
+![]() -
-![]() -
-![]() ,即(
,即(![]() +
+![]() )(
)(![]() -
-![]() -1)=0,因为
-1)=0,因为![]() +
+![]() >0,所以
>0,所以![]() -
-![]() =1(n≥2).由等差数列的定义即可得出;
=1(n≥2).由等差数列的定义即可得出;
(2)利用等差数列的前n项和公式求出![]() 则
则![]() 通过“裂项求和”即可得出
通过“裂项求和”即可得出![]() .
.
试题解析:
(1)证明 ∵![]() =
=![]() ,n∈N*,
,n∈N*,
∴当n=1时, ![]() =
=![]() =
=![]() (
(![]() >0),∴a1=1.当n≥2时,由
>0),∴a1=1.当n≥2时,由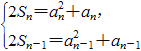
得2![]() =a
=a![]() +
+![]() -a
-a![]() -
-![]() ,即(
,即(![]() +
+![]() )(
)(![]() -
-![]() -1)=0,∵
-1)=0,∵![]() +
+![]() >0,∴
>0,∴![]() -
-![]() =1(n≥2).所以数列{an}是以1为首项,1为公差的等差数列.
=1(n≥2).所以数列{an}是以1为首项,1为公差的等差数列.
(2)解 由(1)可得![]() =n,
=n, ![]() =
=![]() ,∴
,∴![]() =
=![]() =
=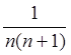 =
=![]() -
-![]() .
.
∴![]() =1-
=1-![]() +
+![]() -
-![]() +…+
+…+![]() -
-![]() =1-
=1-![]() =
=![]() .
.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案【题目】某商店对新引进的商品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
定价 | 9 | 9.2 | 9.4 | 9.6 | 9.8 | 10 |
销量 | 100 | 94 | 93 | 90 | 85 | 78 |
(1)求回归直线方程![]() ;
;
(2)假设今后销售依然服从(Ⅰ)中的关系,且该商品金价为每件5元,为获得最大利润,商店应该如何定价?(利润=销售收入-成本)
参考公式:![]() .
.
【题目】随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了100位育龄妇女,结果如表.
非一线 | 一线 | 总计 | |
愿生 | 45 | 20 | 65 |
不愿生 | 13 | 22 | 35 |
总计 | 58 | 42 | 100 |
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
由K2= ![]() 算得,K2=
算得,K2= ![]() ≈9.616参照附表,得到的正确结论是( )
≈9.616参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别无关”
C.有99%以上的把握认为“生育意愿与城市级别有关”
D.有99%以上的把握认为“生育意愿与城市级别无关”