题目内容
18．
已知底面为正三角形的三棱柱ABC-A1B1C1中，AA1⊥平面ABC，D、E分别是A1B1，AA1的中点，F是AB边上的点，且FB=3AF，连接EF、DB、C1B、C1D．（Ⅰ）求证：平面BC1D⊥平面ABB1A1；
（Ⅱ）在线段AC上，是否存在一点M，使得平面FEM∥平面BC1D，若存在，请找出点M的位置，并证明平面FEM∥平面BC1D，若不存在，请说明理由．
分析 （Ⅰ）由题意可证明C1D⊥A1B1，又平面ABB1A1∩平面A1B1C1=A1B1，可证C1D⊥平面ABB1A1，即可证明平面BC1D⊥平面ABB1A1．
（Ⅱ）取AB中点O，连接CO，DO，取AC中点M，连接EM，MF，可证四边形C1DOC为平面四边形，F为线段AO中点，可证MF∥C1D，有MF∥平面BC1D，连接A1O，同理可得EF∥平面BC1D，由EF∩MF=F，EF?平面FEM，FM?平面FEM，即可证明平面FEM∥平面BC1D．
解答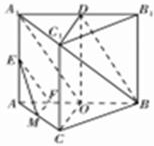 
解：（Ⅰ）由题意可知，平面ABB1A1⊥平面A1B1C1，…1分
因为△A1B1C1为等边三角形，且D为A1B1的中点，故C1D⊥A1B1，…3分
因为平面ABB1A1∩平面A1B1C1=A1B1，故C1D⊥平面ABB1A1，…5分
因为C1D?平面BC1D，故平面BC1D⊥平面ABB1A1…6分
（Ⅱ）当点M为线段AC的中点时，平面FEM∥平面BC1D…7分
如图，取AB中点O，连接CO，DO，取AC中点M，连接EM，MF，
由三棱柱性质可知，四边形C1DOC为平面四边形，
因为FB=3AF，且O为线段AB中点，故F为线段AO中点，
又M为线段AC中点，故MF∥CO，又C1D∥CO，故MF∥C1D，
因为MF?平面BC1D，C1D?平面BC1D，故MF∥平面BC1D，…10分
连接A1O，同理可得EF∥平面BC1D…11分
因为EF∩MF=F，EF?平面FEM，FM?平面FEM，
故平面FEM∥平面BC1D…12分
点评 本题主要考查了面面垂直的判定定理和性质定理，线面平行的判定定理，面面平行的判定定理，考查了转化与化归思想，空间想象能力和推论论证能力，属于中档题．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
9．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一个焦点与抛物线y2=4x的焦点重合，且椭圆的离心率等于$\frac{\sqrt{3}}{2}$，则该椭圆的方程为（ ）
| A． | $\frac{4{x}^{2}}{5}$+5y2=1 | B． | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | C． | $\frac{4{x}^{2}}{5}$$+\frac{5{y}^{2}}{3}$=1 | D． | $\frac{3}{4}$x2+3y2=1 |
在四棱锥P-ABCD中，底面ABCD是直角梯形，AD∥BC，AB⊥BC，BD⊥DC，侧面PAB⊥底面ABCD，PA=AD=AB，点M是PB的中点．
13．在正方体EFGH-E1F1G1H1中，下列四对截面中，彼此平行的一对截面是（ ）
| A． | 平面E1FG1与平面EGH1 | B． | 平面FHG1与平面F1H1G | ||
| C． | 平面F1H1H与平面FHE1 | D． | 平面E1HG1与平面EH1G |
7．已知曲线y=f（x）在点（1，f（1））处的切线方程为2x-y+2=0，则f′（1）=（ ）
| A． | 4 | B． | -4 | C． | -2 | D． | 2 |