题目内容
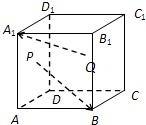
(理)如图,单位正方体ABCD-A1B1C1D1,E,F分别是棱C1D1和B1C1的中点,试求:
(Ⅰ)AF与平面BEB1所成角的余弦值;
(Ⅱ)点A到面BEB1的距离.
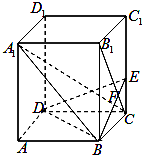
(Ⅰ)AF与平面BEB1所成角的余弦值;
(Ⅱ)点A到面BEB1的距离.

(1)如图所示,建立空间直角坐标系.
 则A(1,0,0),B(1,1,0),B1(1,1,1),E(0,
则A(1,0,0),B(1,1,0),B1(1,1,1),E(0,
,1),F(
,1,1).
∴
=(0,0,1),
=(-1,-
,1),
=(-
,1,1).
设平面BEB1的法向量为
=(x,y,z),
则
,即
,取y=2,则x=-1,z=0.
∴
=(-1,2,0),
设AF与平面BEB1所成的角为θ,θ∈[0,
].
则sinθ=|cos<
,
>|=
=
=
,
∴cosθ=
=
.
(2)由(1)可得平面BEB1的法向量
=(-1,2,0),
=(0,1,0).
∴点A到面BEB1的距离d=
=
=
.
 则A(1,0,0),B(1,1,0),B1(1,1,1),E(0,
则A(1,0,0),B(1,1,0),B1(1,1,1),E(0,| 1 |
| 2 |
| 1 |
| 2 |
∴
| BB1 |
| BE |
| 1 |
| 2 |
| AF |
| 1 |
| 2 |
设平面BEB1的法向量为
| n |
则
|
|
∴
| n |
设AF与平面BEB1所成的角为θ,θ∈[0,
| π |
| 2 |
则sinθ=|cos<
| n |
| AF |
|
| ||||
|
|
| ||||||
|
| ||
| 3 |
∴cosθ=
| 1-sin2θ |
| 2 |
| 3 |
(2)由(1)可得平面BEB1的法向量
| n |
| AB |
∴点A到面BEB1的距离d=
|
| ||||
|
|
| 2 | ||
|
2
| ||
| 5 |

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目