题目内容
(本小题满分12分)已知椭圆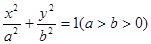 ,离心率为
,离心率为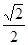 的椭圆经过点
的椭圆经过点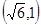 .
.
(1)求该椭圆的标准方程;
(2)过椭圆的一个焦点且互相垂直的直线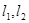 分别与椭圆交于
分别与椭圆交于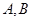 和
和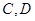 ,是否存在常数
,是否存在常数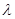 ,使得
,使得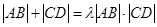 ?若存在,求出实数
?若存在,求出实数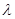 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
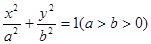 ,离心率为
,离心率为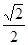 的椭圆经过点
的椭圆经过点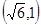 .
.(1)求该椭圆的标准方程;
(2)过椭圆的一个焦点且互相垂直的直线
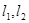 分别与椭圆交于
分别与椭圆交于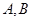 和
和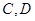 ,是否存在常数
,是否存在常数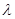 ,使得
,使得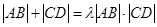 ?若存在,求出实数
?若存在,求出实数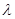 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(1) (2)存在实数
(2)存在实数 ,使得
,使得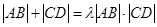 .理由见解析
.理由见解析
 (2)存在实数
(2)存在实数 ,使得
,使得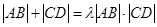 .理由见解析
.理由见解析试题分析:(1)由题可知
 ,即
,即 ,
,由此得
 ,故椭圆方程是
,故椭圆方程是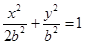 ,
,将点
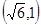 的坐标代入,得
的坐标代入,得 ,解得
,解得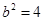 ,
,故椭圆方程是
 . ……4分
. ……4分(2)问题等价于
 ,即
,即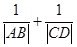 是否是定值问题.
是否是定值问题.椭圆的焦点坐标是
 ,不妨取焦点
,不妨取焦点 ,
,当直线
 的斜率存在且不等于零时,
的斜率存在且不等于零时,设直线
 的斜率为
的斜率为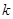 ,则直线
,则直线 的方程是
的方程是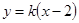 ,
,代入椭圆方程并整理得

设
 ,则
,则 . ……6分
. ……6分根据弦长公式,
 =
=
=
 =
= ……8分
……8分以
 代换
代换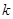 ,得
,得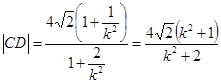 ……9分
……9分所以

即
 ……10分
……10分当直线
 的斜率不存在或等于零时,
的斜率不存在或等于零时,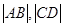 一个是椭圆的长轴长,一个是通径长度,
一个是椭圆的长轴长,一个是通径长度,此时
 ,即
,即 .
.综上所述,故存在实数
 ,使得
,使得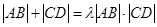 . ……12分
. ……12分点评:圆锥曲线问题一般难度较大,要仔细分析,仔细运算,另外设直线方程时,要考虑到直线的斜率是否存在.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 交抛物线
交抛物线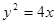 于A(x1,y1),B(x2,y2)两点,抛物线的顶点是
于A(x1,y1),B(x2,y2)两点,抛物线的顶点是 .
.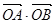 为定值;
为定值; 与抛物线
与抛物线 的准线围成的三角形区域(包含边界)为
的准线围成的三角形区域(包含边界)为 ,
, 为
为 的最大值为( )
的最大值为( )


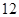
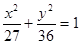 有相同焦点,且经过点
有相同焦点,且经过点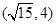 ,
,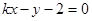 与曲线
与曲线 有两个不同的交点,则实数
有两个不同的交点,则实数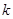 的取值范围是( )
的取值范围是( )



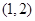 总可作两条直线与圆
总可作两条直线与圆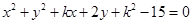 相切,则实数
相切,则实数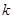 的取值范围是 .
的取值范围是 .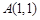 是椭圆
是椭圆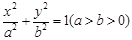 上一点,
上一点,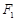 ,
,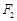 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足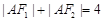
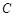 、
、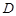 是椭圆上任两点,且直线
是椭圆上任两点,且直线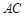 、
、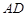 的斜率分别为
的斜率分别为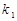 、
、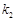 ,若存在常数
,若存在常数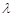 使
使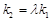 ,求直线
,求直线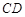 的斜率.
的斜率.  有共同焦点,且过点(0,2)的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程.
有共同焦点,且过点(0,2)的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程. 的棱长为
的棱长为 ,点
,点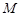 在棱
在棱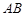 上, 且
上, 且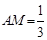 , 点
, 点 是平面
是平面 上的动点,且动点
上的动点,且动点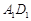 的距离与点
的距离与点