题目内容
16.椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点与短轴的两端点的连线互相垂直,且此焦点和长轴上较近的端点距离为4$\sqrt{3}$-2$\sqrt{6}$,则此椭圆方程为$\frac{{x}^{2}}{48}$+$\frac{{y}^{2}}{24}$=1.分析 由题意可得b=c,a-c=4$\sqrt{3}$-2$\sqrt{6}$,又a2-c2=b2,解方程可得a,b的值,进而得到椭圆方程.
解答 解:一个焦点与短轴的两端点的连线互相垂直,
即有焦点与短轴的两端点构成一个等腰直角三角形,
即有b=c,
又此焦点和长轴上较近的端点距离为4$\sqrt{3}$-2$\sqrt{6}$,
即为a-c=4$\sqrt{3}$-2$\sqrt{6}$,
又a2-c2=b2,
解得a=4$\sqrt{3}$,b=c=2$\sqrt{6}$,
则椭圆方程为$\frac{{x}^{2}}{48}$+$\frac{{y}^{2}}{24}$=1.
故答案为:$\frac{{x}^{2}}{48}$+$\frac{{y}^{2}}{24}$=1.
点评 本题考查椭圆的方程和性质,主要考查椭圆方程的求法,注意运用方程的思想方法,属于基础题.

练习册系列答案
相关题目
11.已知一个底面是菱形的直棱柱的侧棱长为5,菱形的对角线的长分别是9和15,则这个棱柱的侧面积是( )
| A. | 30$\sqrt{34}$ | B. | 60$\sqrt{34}$ | C. | 30$\sqrt{34}$+135 | D. | 135 |
1.圆台的上、下底面面积分别为4和16,中截面把圆台分成两部分,则这两部分的体积之比为( )
| A. | 37:8 | B. | 8:27 | C. | 27:64 | D. | 19:37 |
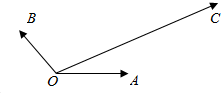 如图|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°,|$\overrightarrow{OC}$|=5,则$\overrightarrow{OC}$=$\frac{10\sqrt{3}}{3}$$\overrightarrow{OA}$+$\frac{5\sqrt{3}}{3}$$\overrightarrow{OB}$.(用$\overrightarrow{OA}和\overrightarrow{OB}$表示)
如图|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°,|$\overrightarrow{OC}$|=5,则$\overrightarrow{OC}$=$\frac{10\sqrt{3}}{3}$$\overrightarrow{OA}$+$\frac{5\sqrt{3}}{3}$$\overrightarrow{OB}$.(用$\overrightarrow{OA}和\overrightarrow{OB}$表示)
 如图,在△ABC中,∠ACB的平分线CD交AB于D,$\overrightarrow{AC}$的模为2,$\overrightarrow{BC}$的模为3,$\overrightarrow{AD}$的模为1,那么$\overrightarrow{DB}$的模为$\frac{3}{2}$.
如图,在△ABC中,∠ACB的平分线CD交AB于D,$\overrightarrow{AC}$的模为2,$\overrightarrow{BC}$的模为3,$\overrightarrow{AD}$的模为1,那么$\overrightarrow{DB}$的模为$\frac{3}{2}$.