题目内容
8.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线与曲线y=x3+2相切,则双曲线的离心率为$\sqrt{10}$.分析 求出双曲线的渐近线方程,函数y=x3+2,求导函数,再设切点坐标,利用双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与曲线y=x3+2相切,建立方程组,即可求得几何量之间的关系,从而可求双曲线的离心率.
解答 解:双曲线的渐近线方程为y=±$\frac{b}{a}$x,函数y=x3+2,求导函数可得y=3x2,
设切点坐标为(m,n),则
∵双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与曲线y=x3+2相切,
∴$\left\{\begin{array}{l}{n=3{m}^{2}}\\{n=\frac{b}{a}m}\\{3{m}^{2}=\frac{b}{a}}\end{array}\right.$,∴m=1,$\frac{b}{a}$=3,∴b=3a,
∴c2=a2+b2=10a2,
∴c=$\sqrt{10}$a,
∴e=$\frac{c}{a}$=$\sqrt{10}$
故答案为:$\sqrt{10}$.
点评 本题考查直线与曲线相切,考查双曲线的几何性质,正确运用双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与曲线y=x3+2相切是关键.

练习册系列答案
相关题目
13. 如图是利用斜二测画法画出的△ABO的直观图,已知O′B′=4,且△ABO的面积为16,过A′作A′C′⊥x′轴,则A′C′的长为( )
如图是利用斜二测画法画出的△ABO的直观图,已知O′B′=4,且△ABO的面积为16,过A′作A′C′⊥x′轴,则A′C′的长为( )
 如图是利用斜二测画法画出的△ABO的直观图,已知O′B′=4,且△ABO的面积为16,过A′作A′C′⊥x′轴,则A′C′的长为( )
如图是利用斜二测画法画出的△ABO的直观图,已知O′B′=4,且△ABO的面积为16,过A′作A′C′⊥x′轴,则A′C′的长为( )| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $16\sqrt{2}$ | D. | 1 |
20.口袋中有20个球,其中白球9个,红球5个,黑球6个,现从中任取10个球,使得白球不少于2个但不多于8个,红球不少于2个,黑球不多于3个,那么上述取法的种数是( )
| A. | 14 | B. | 16 | C. | 18 | D. | 20 |
17.已知某几何体的三视图如图所示,其中俯视图是扇形,则该几何体的体积为( )
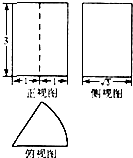

| A. | 4 π | B. | 2 π | C. | $\frac{4π}{3}$ | D. | $\frac{2π}{3}$ |
