题目内容
17.实数x,y满足$\left\{{\begin{array}{l}{x-y+1≥0}\\{x+3y-3≥0}\\{3x+y-9≤0}\end{array}}\right.$,则z=ax+y的最大值为2a+3,则a的取值范围是( )| A. | [-3,1] | B. | [-1,3] | C. | [3,+∞) | D. | (-∞,-1] |
分析 本题考查的知识点是简单线性规划的应用,我们要先画出满足约束条件的平面区域,然后分析平面区域里各个角点,进一步分目标函数z=ax+y的最大值为a+3,构造一个关于a的不等式,解不等式即可求出a的范围.
解答 解:由变量x,y满足约束条件$\left\{{\begin{array}{l}{x-y+1≥0}\\{x+3y-3≥0}\\{3x+y-9≤0}\end{array}}\right.$,
作出可行域:
∵z=ax+y,A(0,1),∴zA=1;
解方程组$\left\{\begin{array}{l}{x-y+1=0}\\{3x+y-9=0}\end{array}\right.$,得B(2,3),∴zB=2a+3;
C(3,0),∴zC=3a.
∵线性目标函数z=ax+y的最大值为2a+3,
∴$\left\{\begin{array}{l}{2a+3≥3a}\\{2a+3≥1}\end{array}\right.$,解得-1≤a≤3.
故选:B.
点评 在解决线性规划的小题时,我们常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.

练习册系列答案
相关题目
7. 如图是一个旋转体的三视图,其中正视图,侧视图都是由半圆和矩形组成,则这个旋转体的体积是( )
如图是一个旋转体的三视图,其中正视图,侧视图都是由半圆和矩形组成,则这个旋转体的体积是( )
 如图是一个旋转体的三视图,其中正视图,侧视图都是由半圆和矩形组成,则这个旋转体的体积是( )
如图是一个旋转体的三视图,其中正视图,侧视图都是由半圆和矩形组成,则这个旋转体的体积是( )| A. | $\frac{8}{3}$π | B. | $\frac{7}{3}$π | C. | 2π | D. | $\frac{5}{3}$π |
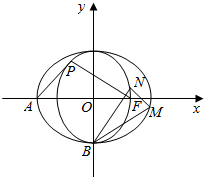 已知椭圆C1:$\frac{{x}^{2}}{2}$+y2=1和圆C2:x2+y2=1,A,B,F分别为椭圆C1左顶点、下顶点和右焦点.
已知椭圆C1:$\frac{{x}^{2}}{2}$+y2=1和圆C2:x2+y2=1,A,B,F分别为椭圆C1左顶点、下顶点和右焦点.