题目内容
17．若cosθ＜0，且cosθ-sinθ=$\sqrt{1-2sinθcosθ}$，那么θ是（ ）| A． | 第一象限角 | B． | 第二象限角 | C． | 第三象限角 | D． | 第四象限角 |
分析 利用三角函数的基本关系式将等式化简，得到sinθ，cosθ的大小，判断θ位置．
解答 解：因为cosθ-sinθ=$\sqrt{1-2sinθcosθ}$=|sinθ-cosθ|，所以cosθ＞sinθ，又cosθ＜0，所以sinθ＜0，
所以θ在第三象限；
故选C
点评 本题考查了三角函数基本关系式的运用以及利用三角函数符号判断角的位置；属于基础题．
练习册系列答案
相关题目
5．下图所示的圆锥的俯视图为（ ）
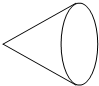
| A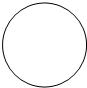． |  | B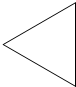． |  | C． |  | D． |  |
12．已知函数f（x）=（m2-m-1）x-5m-3是幂函数，且在区间（0，+∞）上是增函数，则m的值为（ ）
| A． | -1 | B． | 2 | C． | 2或-1 | D． | 0或-1 |
9．在△ABC中，角A，B，C所对的边分别为a，b，c，已知b2-2c2-bc=0，a=$\sqrt{6}$，cosA=$\frac{7}{8}$，则△ABC的面积S为（ ）
| A． | $\frac{8\sqrt{15}}{5}$ | B． | $\sqrt{15}$ | C． | $\frac{\sqrt{15}}{2}$ | D． | 6$\sqrt{3}$ |
6．
据《南通日报》报道，2015年1月1日至1月31日，市交管部门共抽查了1000辆车，查出酒后驾车和醉酒驾车的驾驶员80人，如图是对这80人血液中酒精含量进行检查所得结果的频率分布直方图．（酒精含量≥80mg/100ml为醉酒驾车）
（1）根据频率分布直方图完成下表：
（2）根据上述数据，求此次抽查的1000人中属于醉酒驾车的概率；
（3）若用分层抽样的方法从血液酒精浓度在[70，90）范围内的驾驶员中抽取一个容量为5的样本，并将该样本看成一个总体，从中任取2人，求恰有1人属于醉酒驾车的概率．
据《南通日报》报道，2015年1月1日至1月31日，市交管部门共抽查了1000辆车，查出酒后驾车和醉酒驾车的驾驶员80人，如图是对这80人血液中酒精含量进行检查所得结果的频率分布直方图．（酒精含量≥80mg/100ml为醉酒驾车）（1）根据频率分布直方图完成下表：
| 酒精含量（单位：mg/100ml） | [20，30） | [30，40） | [40，50） | [50，60） |
| 人数 | 16 | 16 | 4 | |
| 酒精含量（单位：mg/100ml） | [60，70） | [70，80） | [80，90） | [90，100] |
| 人数 | 4 |
（3）若用分层抽样的方法从血液酒精浓度在[70，90）范围内的驾驶员中抽取一个容量为5的样本，并将该样本看成一个总体，从中任取2人，求恰有1人属于醉酒驾车的概率．