题目内容
19.已知以原点O为中心的椭圆C上一点到两焦点F1(-$\sqrt{7}$,0),F2($\sqrt{7}$,0)的距离之和为8.(1)求椭圆C的方程;
(2)设P、Q是椭圆C上两点,且$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,求点O到弦PQ的距离.
分析 (1)设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),从而可得2a=8,c=$\sqrt{7}$,从而解椭圆的方程;
(2)设P(x1,y1),Q(x2,y2);则由$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0得$\overrightarrow{OP}$⊥$\overrightarrow{OQ}$,分点P、Q在坐标轴上与点P、Q不在坐标轴上讨论,从而分别求点O到弦PQ的距离,从而解得.
解答 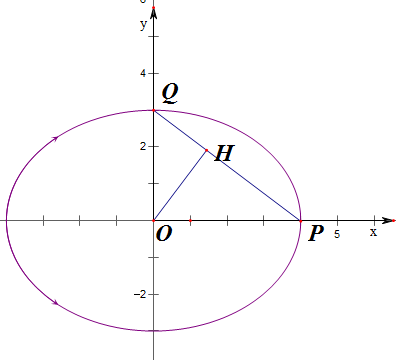 解:(1)设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
解:(1)设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
依题意,2a=8,c=$\sqrt{7}$,
故b2=16-7=9;
故椭圆C的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1;
(2)设P(x1,y1),Q(x2,y2);
则由$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0得$\overrightarrow{OP}$⊥$\overrightarrow{OQ}$,
①当点P、Q在坐标轴上时,不妨设点P在x轴上,
点Q在y轴上,过O作OH⊥PQ于点H,
可得|OH|=$\frac{12}{5}$;
②当点P、Q不在坐标轴上时,
设直线OP的方程为y=kx,则直线OQ的方程为y=-$\frac{1}{k}$x;
将y=kx代入椭圆方程$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1得,
${x}_{1}^{2}$=$\frac{144}{16{k}^{2}+9}$,
∴|OP|2=${x}_{1}^{2}$+${y}_{1}^{2}$=$\frac{144({k}^{2}+1)}{16{k}^{2}+9}$,
同理可得,|OQ|2=$\frac{144({k}^{2}+1)}{9{k}^{2}+16}$;
又在Rt△POQ中作OH⊥PQ于点H,
于是由|OH|•|PQ|=|OP|•|OQ|得,
|OH|2=$\frac{|OP{|}^{2}•|OQ{|}^{2}}{|PQ{|}^{2}}$
=$\frac{|OP{|}^{2}•|OQ{|}^{2}}{|OP{|}^{2}+|OQ{|}^{2}}$
=$\frac{144}{25}$;
故|OH|=$\frac{12}{5}$;
综上所述,所求椭圆中心O到弦PQ的距离为$\frac{12}{5}$.
点评 本题考查了椭圆的方程的求法及椭圆与直线的位置关系及应用,属于中档题.

| A. | {2} | B. | (-3,3) | C. | (1,3) | D. | {1,2} |
| A. | 3 | B. | 3$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 6 |