题目内容
9.已知正方体ABCD-A1B1C1D1的棱长为l,动点P在正方体表面上且满足|PA|=|PC1|,则动点P的轨迹长度为( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 6 |
分析 首先以边D1A1,D1C1,D1D所在直线为x轴,y轴,z轴建立空间直角坐标系,得到A(1,0,1),C1(0,1,0),由于动点P在正方体的表面上,所以可讨论P点在正方体各面上的情况.这时候,可先来看一下P点在平面ABCD上的情况,这样设P(x0,y0,1),根据条件|PA|=|PC1|得到${y}_{0}={x}_{0}+\frac{1}{2}$,所以这时可建立平面直角坐标系,从而找出直线${y}_{0}={x}_{0}+\frac{1}{2}$和正方体边的交点,从而找到P点在该平面上的轨迹为一条线段,并可求出该线段长度为$\frac{\sqrt{2}}{2}$,而同理P点在其它平面上时求法一样,且都为$\frac{\sqrt{2}}{2}$,这样便可求P点轨迹的长度.
解答 解:如图,分别以边D1A1,D1C1,D1D所在直线为x轴,y轴,z轴建立空间直角坐标系;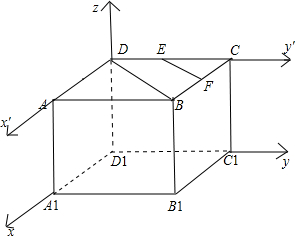 可以以下两点坐标:
可以以下两点坐标:
A(1,0,1),C1(0,1,0);
若P点在正方形ABCD内,设P(x0,y0,1);
∴由|PA|=|PC1|得:
$({x}_{0}-1)^{2}+{{y}_{0}}^{2}={{x}_{0}}^{2}+({y}_{0}-1)^{2}+1$;
∴${y}_{0}={x}_{0}+\frac{1}{2}$;
分别以边DA,DC为x′轴,y′轴建立平面直角坐标系;
直线${y}_{0}={x}_{0}+\frac{1}{2}$就是直线EF,所以在该平面上的P点的轨迹是线段EF,且|EF|=$\frac{\sqrt{2}}{2}$;
同理可求P点在其它平面上时P点的轨迹也是线段,且长度都为$\frac{\sqrt{2}}{2}$;
∴动点P的轨迹长度为$\frac{\sqrt{2}}{2}×6=3\sqrt{2}$.
故选B.
点评 考查建立空间直角坐标系,平面直角坐标系解决问题的方法,会确定空间点的坐标,空间两点之间的距离公式,以及平面直角坐标系中的直线方程.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案| A. | $\frac{33}{65}$ | B. | $\frac{56}{65}$ | C. | -$\frac{33}{65}$ | D. | -$\frac{56}{65}$ |
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| 件数x(件) | 11 | 12 | 13 |
| 时间y(小时) | 25 | 26 | 30 |
(2)试预测同时生产20件该产品需要多少小时?
(附:线性回归方程$\widehat{y}$=bx+a中,b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}-b\overline{x}$)
 如图,已知椭圆C的中心在原点,焦点 F1,F2在x轴上,焦距与短轴长均为2$\sqrt{2}$.
如图,已知椭圆C的中心在原点,焦点 F1,F2在x轴上,焦距与短轴长均为2$\sqrt{2}$.