题目内容
(本题满分10分)
(理)红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛,甲对A,乙对B,丙对C各一盘,已知甲胜A,乙胜B,丙胜C的概率分别为0.6,0.5,0.5,假设各盘比赛结果相互独立.(Ⅰ)求红队至少两名队员获胜的概率;
(Ⅱ)用 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求 的分布列和数学期望
的分布列和数学期望 .
.
(理)红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛,甲对A,乙对B,丙对C各一盘,已知甲胜A,乙胜B,丙胜C的概率分别为0.6,0.5,0.5,假设各盘比赛结果相互独立.(Ⅰ)求红队至少两名队员获胜的概率;
(Ⅱ)用
 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求 的分布列和数学期望
的分布列和数学期望 .
.(1)0.55;(2)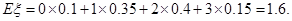
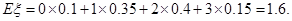
(I)设甲胜A的事件为D,乙胜B的事件为E,丙胜C的事件为F,则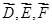 分别表示甲不胜A、乙不胜B,丙不胜C的事件.解决本小题的关键是搞清楚“红队至少两名队员获胜”包括
分别表示甲不胜A、乙不胜B,丙不胜C的事件.解决本小题的关键是搞清楚“红队至少两名队员获胜”包括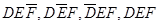 四个基本事件.
四个基本事件.
(II)确定出 可能的取值为0,1,2,3是解决问题的第一步,然后求出每个值对应的概率,列出分布列,再根据分布列求期望.期望=每一个
可能的取值为0,1,2,3是解决问题的第一步,然后求出每个值对应的概率,列出分布列,再根据分布列求期望.期望=每一个 值与其对应的概率积之和.
值与其对应的概率积之和.
解:(理)(I)设甲胜A的事件为D,乙胜B的事件为E,丙胜C的事件为F,则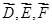 分别表示甲不胜A、乙不胜B,丙不胜C的事件.
分别表示甲不胜A、乙不胜B,丙不胜C的事件.
因为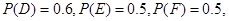
由对立事件的概率公式知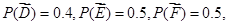
红队至少两人获胜的事件有: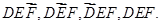
由于以上四个事件两两互斥且各盘比赛的结果相互独立,………………………………2分
因此红队至少两人获胜的概率为
 ……6分
……6分
(II)由题意知 可能的取值为0,1,2,3.
可能的取值为0,1,2,3.
又由(I)知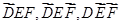 是两两互斥事件,
是两两互斥事件,
且各盘比赛的结果相互独立,
因此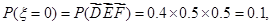
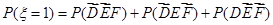
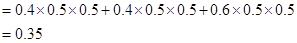
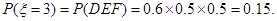
由对立事件的概率公式得
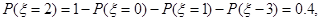 ……………………9分
……………………9分
所以 的分布列为:
的分布列为:
因此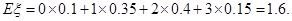 ……………………10分
……………………10分
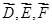 分别表示甲不胜A、乙不胜B,丙不胜C的事件.解决本小题的关键是搞清楚“红队至少两名队员获胜”包括
分别表示甲不胜A、乙不胜B,丙不胜C的事件.解决本小题的关键是搞清楚“红队至少两名队员获胜”包括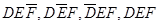 四个基本事件.
四个基本事件.(II)确定出
 可能的取值为0,1,2,3是解决问题的第一步,然后求出每个值对应的概率,列出分布列,再根据分布列求期望.期望=每一个
可能的取值为0,1,2,3是解决问题的第一步,然后求出每个值对应的概率,列出分布列,再根据分布列求期望.期望=每一个 值与其对应的概率积之和.
值与其对应的概率积之和.解:(理)(I)设甲胜A的事件为D,乙胜B的事件为E,丙胜C的事件为F,则
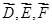 分别表示甲不胜A、乙不胜B,丙不胜C的事件.
分别表示甲不胜A、乙不胜B,丙不胜C的事件.因为
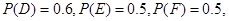
由对立事件的概率公式知
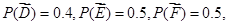
红队至少两人获胜的事件有:
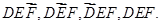
由于以上四个事件两两互斥且各盘比赛的结果相互独立,………………………………2分
因此红队至少两人获胜的概率为
 ……6分
……6分(II)由题意知
 可能的取值为0,1,2,3.
可能的取值为0,1,2,3.又由(I)知
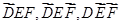 是两两互斥事件,
是两两互斥事件,且各盘比赛的结果相互独立,
因此
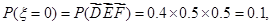
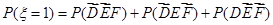
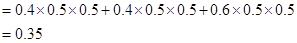
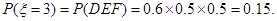
由对立事件的概率公式得
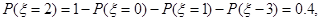 ……………………9分
……………………9分所以
 的分布列为:
的分布列为: | 0 | 1 | 2 | 3 |
| P | 0.1 | 0.35 | 0.4 | 0.15 |
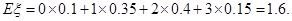 ……………………10分
……………………10分
练习册系列答案
相关题目




 和
和 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中: 的分布列与期望.
的分布列与期望.



 是一个随机变量,求随机变量
是一个随机变量,求随机变量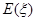 .
. 个男生和
个男生和 个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有
个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有 种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有
种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有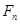 种选法.
种选法. 和
和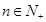 ),并用数学归纳法证明.
),并用数学归纳法证明. 视觉
视觉 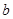

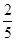 .
. ,求随机变量
,求随机变量 .
.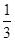 ,某
,某 表示四次实验结束时实验成功的次数与失败的次数之差的绝对
表示四次实验结束时实验成功的次数与失败的次数之差的绝对 ;
; 的解集是实数集
的解集是实数集 ”为事件
”为事件 ,求事件
,求事件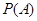 .
.