题目内容
某班级共派出 个男生和
个男生和 个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有
个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有 种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有
种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有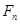 种选法.
种选法.
(1)试求 和
和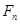 ;
;
(2)判断 和
和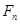 的大小(
的大小(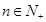 ),并用数学归纳法证明.
),并用数学归纳法证明.
 个男生和
个男生和 个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有
个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有 种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有
种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有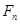 种选法.
种选法.(1)试求
 和
和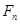 ;
; (2)判断
 和
和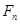 的大小(
的大小(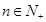 ),并用数学归纳法证明.
),并用数学归纳法证明.(1) ,
,
(2)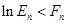
 ,
,
(2)
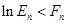
(1)根据排列和组合知识求出 和
和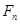 ;(2)先根据前几个特殊项猜想出结果,然后利用数学归纳法的步骤去证明,本题在证明n=k+1时,用到了分析法
;(2)先根据前几个特殊项猜想出结果,然后利用数学归纳法的步骤去证明,本题在证明n=k+1时,用到了分析法
解:(1) ,
, .
.
(2)因为 ,所以
,所以 ,
, ,
, ,由此猜想:当
,由此猜想:当 时,都有
时,都有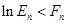 ,即
,即 .
.
下面用数学归纳法证明 (
( ).
).
1) 当 时,该不等式显然成立.
时,该不等式显然成立.
2) 假设当 时,不等式成立,即
时,不等式成立,即 ,则当
,则当 时,
时, ,要证当
,要证当 时不等式成立.只要证:
时不等式成立.只要证: ,只要证:
,只要证: .
.
令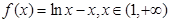 ,因为
,因为 ,所以
,所以 在
在 上单调递减,
上单调递减,
从而 ,而
,而 ,所以
,所以 成立.
成立.
则当 时,不等式也成立.
时,不等式也成立.
综合1)、2)得原不等式对任意的 均成立.
均成立.
 和
和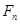 ;(2)先根据前几个特殊项猜想出结果,然后利用数学归纳法的步骤去证明,本题在证明n=k+1时,用到了分析法
;(2)先根据前几个特殊项猜想出结果,然后利用数学归纳法的步骤去证明,本题在证明n=k+1时,用到了分析法解:(1)
 ,
, .
.(2)因为
 ,所以
,所以 ,
, ,
, ,由此猜想:当
,由此猜想:当 时,都有
时,都有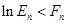 ,即
,即 .
.下面用数学归纳法证明
 (
( ).
).1) 当
 时,该不等式显然成立.
时,该不等式显然成立.2) 假设当
 时,不等式成立,即
时,不等式成立,即 ,则当
,则当 时,
时, ,要证当
,要证当 时不等式成立.只要证:
时不等式成立.只要证: ,只要证:
,只要证: .
.令
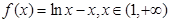 ,因为
,因为 ,所以
,所以 在
在 上单调递减,
上单调递减,从而
 ,而
,而 ,所以
,所以 成立.
成立.则当
 时,不等式也成立.
时,不等式也成立.综合1)、2)得原不等式对任意的
 均成立.
均成立.
练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 ,
, ,且
,且



 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求 .
. ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为 ,
, .
.
 的数学期望;
的数学期望; ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为 ,且各次投篮互不影响.(Ⅰ) 求甲获胜的概率;(Ⅱ)求投篮结束时甲的投篮次数
,且各次投篮互不影响.(Ⅰ) 求甲获胜的概率;(Ⅱ)求投篮结束时甲的投篮次数 的分布列与期望
的分布列与期望 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且 .
.
 ,则使P(ξ=k)取最大值时的k值为( )
,则使P(ξ=k)取最大值时的k值为( ) 的分布规律如下,其中a、b、c为等差数列,若E(
的分布规律如下,其中a、b、c为等差数列,若E( ,则D(
,则D(


