题目内容
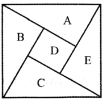
【题目】如图为我国数学家赵爽(约3世纪初)在为《周牌算经》作注时验证勾股定理的示意图,现在提供6种不同的颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则![]() ,
,![]() 区域涂同色的概率为( )
区域涂同色的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
本题从颜色使用数量上来分类,又由条件知至少使用三种颜色,所以只剩三种情况了.然后选色,再按照规定每个区域只涂一种颜色,相邻区域颜色不同,使用分步计数原理逐一涂色,即可求出总的基本事件,再弄清![]() ,
,![]() 区域涂同色的占了多少个基本事件,利用古典概型及其概率计算公式求答案.
区域涂同色的占了多少个基本事件,利用古典概型及其概率计算公式求答案.
解:根据题意,至少使用3种颜色.由使用颜色数量,下面我们分三种情况:
(1)使用5种颜色:选色![]() ,涂上去
,涂上去![]() ,共有
,共有![]() 种;
种;
(2)使用4种颜色:选色![]() ,先涂
,先涂![]() 有4种,下面,①、若
有4种,下面,①、若![]() 、
、![]() 同色,则
同色,则![]() 和
和![]() 各涂剩余的两色,有
各涂剩余的两色,有![]() 种,②、若
种,②、若![]() 、
、![]() 不同色,则
不同色,则![]() 和
和![]() 必同色,有
必同色,有![]() 种.
种.![]() 共
共![]() 种;
种;
(3)使用3种颜色:选色![]() ,先涂
,先涂![]() 有3种选择,
有3种选择,![]() 用掉一种颜色,下面只有
用掉一种颜色,下面只有![]() 、
、![]() 同色,
同色,![]() 、
、![]() 同色,有
同色,有![]() 种,共
种,共![]() 种,
种,
![]() 共计
共计![]() 种,
种,
其中![]() ,
,![]() 区域涂同色的有
区域涂同色的有![]() 种,
种,
则![]() ,
,![]() 区域涂同色的概率为
区域涂同色的概率为![]() .
.
故选:![]() .
.

练习册系列答案
相关题目
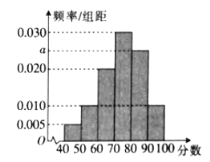
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:

(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|