题目内容
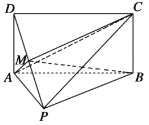
【题目】如图，在边长为4正方体
中，
为
的中点，
，点
在正方体表面上移动，且满足
，则点
和满足条件的所有点构成的图形的面积是______.
【答案】18
【解析】
过点
与直线
垂直的所有直线在过点与垂直的平面上，所以点
的轨迹就是过点与直线垂直的平面与正方体表面的交线.由正方体的垂直关系，可得
平面
，可得
，再确定一条与
相交且与垂直的直线，取
中点
，连
，可证
，则有
平面
，只需确定出平面与正方体表面的交线，取
中点，连
，可证
共面，且为等腰梯形，即为所求的轨迹图形，求其面积，即可求解.
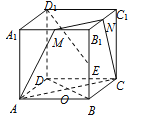
取，的中点分别为，
，
连结，
，
，
由于
，所以
四点共面，
且四边形为梯形，
∵
，
，
，
∴面，∵点在正方体表面上移动，
∴点的运动轨迹为梯形.
∵正方体
的边长为4，
∴
，
，
，
∴梯形为等腰梯形，∴其高为
.
面积为
.
故答案为:18
练习册系列答案
名校课堂系列答案
相关题目
