题目内容
【题目】设椭圆E的方程为![]() (a>b>0),点O为坐标原点,点A的坐标为(a,0),点B的坐标为(0,b),点M在线段AB上,满足BM=2MA,直线OM的斜率为
(a>b>0),点O为坐标原点,点A的坐标为(a,0),点B的坐标为(0,b),点M在线段AB上,满足BM=2MA,直线OM的斜率为![]() .
.
(1)求E的离心率e;
(2)设点C的坐标为(0,-b),N为线段AC的中点,点N关于直线AB的对称点的纵坐标为![]() ,求E的方程.
,求E的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由题意,点![]() 的坐标为
的坐标为![]() ,根据
,根据![]() 的斜率为
的斜率为![]() ,得到
,得到![]() 的关系式,即可求解椭圆的离心率;
的关系式,即可求解椭圆的离心率;
(2)由(1)可得直线![]() 的方程为
的方程为![]() ,得点
,得点![]() 的坐标
的坐标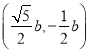 ,解得点
,解得点![]() 关于
关于![]() 点的对称点,列出方程组,求解
点的对称点,列出方程组,求解![]() 的值,进而得到椭圆的方程.
的值,进而得到椭圆的方程.
试题解析:
解 (1)由题设条件知,点M的坐标为![]() ,又kOM=
,又kOM=![]() ,从而
,从而![]() =
=![]() ,
,
进而得a=![]() b,c=
b,c=![]() =2b,故e=
=2b,故e=![]() =
=![]() .
.
(2)由题设条件和(1)的计算结果可得,直线AB的方程为![]() +
+![]() =1,点N的坐标为
=1,点N的坐标为![]() .
.
设点N关于直线AB的对称点S的坐标为![]() ,
,
则线段NS的中点T的坐标为![]() .
.
又点T在直线AB上,且kNS·kAB=-1,
从而有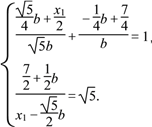 解得b=3.
解得b=3.
所以a=3![]() ,故椭圆E的方程为
,故椭圆E的方程为![]() +
+![]() =1.
=1.

练习册系列答案
相关题目