题目内容

【题目】已知椭圆C： =1（a＞b＞0）的离心率为 ，且经过点（1， ），F1 ， F2是椭圆的左、右焦点．
（1）求椭圆C的方程；
（2）点P在椭圆上运动，求|PF1||PF2|的最大值．

【答案】
（1）解：由题意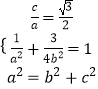，得 ，解得 ．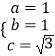

∴椭圆C的方程是


（2）解：∵P在椭圆上运动，

∴|PF1|+|PF2|=2a=4，

∴|PF1||PF2|≤ ，

当且仅当|PF1|=|PF2|时等号成立，

∴|PF1||PF2|的最大值为4


【解析】（1）由已知列关于a，b，c的方程组，求解方程组可得a，b，c的值，则椭圆方程可求；（2）由题意定义可得|PF1|+|PF2|=2a=4，再由基本不等式求得|PF1||PF2|的最大值．

练习册系列答案
相关题目

【题目】在△ABC中，a，b，c分别是角A，B，C的对边，且满足 + =4cosC． （Ⅰ）求 的值；
（Ⅱ）若tanA=2tanB，求sinA的值．

【题目】下列四个命题： ①共线向量是在同一条直线上的向量；
②若两个向量不相等，则它们的终点不可能是同一点；
③与已知非零向量共线的单位向量是唯一的；
④若四边形ABCD是平行四边形，则 与 ， 与 分别共线．
其中正确命题的个数是（ ）
A.1
B.2
C.3
D.4

【题目】已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜ ）的最小正周期为π，且其图象向左平移 个单位后得到函数g（x）=cosωx的图象，则函数f（x）的图象（ ）
A.关于直线x= 对称
B.关于直线x= 对称
C.关于点（ ，0）对称
D.关于点（ ，0）对称

【题目】如图，一个正六角星薄片（其对称轴与水面垂直）匀速地升出水面，直到全部露出水面为止，记时刻t薄片露出水面部分的图形面积为S（t）（S（0）=0），则导函数y=S'（t）的图象大致为（ ）
A.
B.
C.
D.

【题目】如图，矩形ABCD是一个历史文物展览厅的俯视图，点E在AB上，在梯形BCDE区域内部展示文物，DE是玻璃幕墙，游客只能在△ADE区域内参观，在AE上点P处安装一可旋转的监控摄像头，∠MPN为监控角，其中M、N在线段DE（含端点）上，且点M在点N的右下方，经测量得知：AD=6米，AE=6米，AP=2米，∠MPN= ，记∠EPM=θ（弧度），监控摄像头的可视区域△PMN的面积为S平方米．
（1）求S关于θ的函数关系式，并写出θ的取值范围：（参考数据：tan ≈3）
（2）求S的最小值．

【题目】在某校统考中，甲、乙两班数学学科前10名的成绩如表：
（I）若已知甲班10位同学数学成绩的中位数为125，乙班10位同学数学成绩的平均分为130，求x，y的值；
（Ⅱ）设定分数在135分之上的学生为数学尖优生，从甲、乙两班的所有数学尖优生中任两人，求两人在同一班的概率．

【题目】在△ABC中，角A，B，C的对边分别为a，b，c，若b（tanA+tanB）= ctanB，BC边的中线长为1，则a的最小值为 ．

【题目】设不等式组 所表示的平面区域为Dn ， 记Dn内的整点个数为an（n∈N*）．（整点即横坐标和纵坐标均为整数的点）
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）记数列{an}的前n项和为Sn ， 且 ，若对于一切的正整数n，总有Tn≤m，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网