题目内容
【题目】如图,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在△ADE区域内参观,在AE上点P处安装一可旋转的监控摄像头,∠MPN为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方,经测量得知:AD=6米,AE=6米,AP=2米,∠MPN= ![]() ,记∠EPM=θ(弧度),监控摄像头的可视区域△PMN的面积为S平方米.
,记∠EPM=θ(弧度),监控摄像头的可视区域△PMN的面积为S平方米. 
(1)求S关于θ的函数关系式,并写出θ的取值范围:(参考数据:tan ![]() ≈3)
≈3)
(2)求S的最小值.
【答案】
(1)解:在△PME中,∠EPM=θ,PE=4m,∠PEM= ![]() ,∠PME=
,∠PME= ![]() ,
,
由正弦定理可得PM= ![]() =
= ![]() ,
,
同理,在△PNE中,PN= ![]() ,
,
∴S△PMN= ![]() =
= ![]() =
= 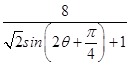 ,
,
M与E重合时,θ=0,N与D重合时,tan∠APD=3,即θ= ![]() ,
,
∴0≤θ≤ ![]() ,
,
综上所述,S△PMN= 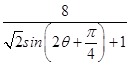 ,0≤θ≤
,0≤θ≤ ![]() ;
;
(2)解:当2θ+ ![]() =
= ![]() 即
即 ![]() 时,S取得最小值
时,S取得最小值 ![]() =8(
=8( ![]() ﹣1)平方米.
﹣1)平方米.
【解析】(1)利用正弦定理,求出PM,PN,即可求S关于θ的函数关系式,M与E重合时,θ=0,N与D重合时,tan∠APD=3,即θ= ![]() ,即可写出θ的取值范围;(2)当2θ+
,即可写出θ的取值范围;(2)当2θ+ ![]() =
= ![]() 即
即 ![]() 时,S取得最小值.
时,S取得最小值.

练习册系列答案
相关题目