题目内容
函数y=(x2-1)3+1在x=-1处
| A.有极大值 | B.无极值 |
| C.有极小值 | D.无法确定极值情况 |
B
本题考查导数与极值的关系,即某一点是极值点的充分条件是这点两侧的导数异号.
y=(x2-1)3+1=[(x2-1)+1][(x2-1)2-(x2-1)+1]=x2(x4-3x2+3)=x6-3x4+3x2.
∴y′=6x5-12x3+6x.令y′=0,x(x2-1)2=0,即x=0,-1,1.
当x<-1时,y′<0;当-1<x<0时,y′<0.
∴x=-1不是极值点.
y=(x2-1)3+1=[(x2-1)+1][(x2-1)2-(x2-1)+1]=x2(x4-3x2+3)=x6-3x4+3x2.
∴y′=6x5-12x3+6x.令y′=0,x(x2-1)2=0,即x=0,-1,1.
当x<-1时,y′<0;当-1<x<0时,y′<0.
∴x=-1不是极值点.

练习册系列答案
相关题目
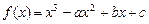 的图象为曲线E.
的图象为曲线E.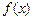 可以在
可以在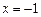 和
和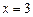 时取得极值,并求此时a,b的值;
时取得极值,并求此时a,b的值;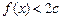 在
在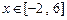 恒成立,求c的取值范围.
恒成立,求c的取值范围.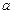 为实数,函数
为实数,函数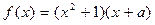 ,若
,若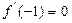 ,求函数
,求函数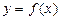 在
在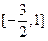 上的最大值和最小值。
上的最大值和最小值。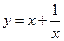 在
在 时有( )
时有( )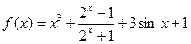 在区间[
在区间[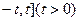 上的最大值与最小值的和 .
上的最大值与最小值的和 .