题目内容
已知函数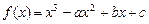 的图象为曲线E.
的图象为曲线E.
(Ⅰ) 若曲线E上存在点P,使曲线E在P点处的切线与x轴平行,求a,b的关系;
(Ⅱ) 说明函数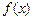 可以在
可以在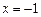 和
和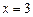 时取得极值,并求此时a,b的值;
时取得极值,并求此时a,b的值;
(Ⅲ) 在满足(2)的条件下,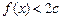 在
在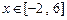 恒成立,求c的取值范围.
恒成立,求c的取值范围.
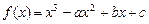 的图象为曲线E.
的图象为曲线E.(Ⅰ) 若曲线E上存在点P,使曲线E在P点处的切线与x轴平行,求a,b的关系;
(Ⅱ) 说明函数
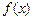 可以在
可以在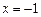 和
和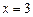 时取得极值,并求此时a,b的值;
时取得极值,并求此时a,b的值;(Ⅲ) 在满足(2)的条件下,
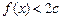 在
在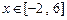 恒成立,求c的取值范围.
恒成立,求c的取值范围.(1) 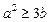 .
.
(2)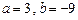 .
.
(3)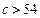 .
.
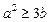 .
.(2)
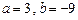 .
. (3)
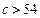 .
. (1) 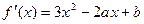 ,设切点为
,设切点为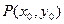 ,则曲线
,则曲线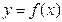 在点P的切线的斜率
在点P的切线的斜率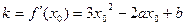 ,由题意知
,由题意知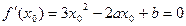 有解,
有解,
∴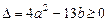 即
即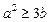 .
.
(2)若函数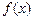 可以在
可以在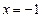 和
和 时取得极值,
时取得极值,
则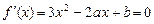 有两个解
有两个解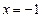 和
和 ,且满足
,且满足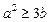 .
.
易得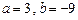 .
.
(3)由(2),得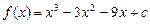 .
.
根据题意,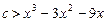 (
(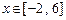 )恒成立.
)恒成立.
∵函数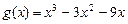 (
(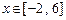 )在
)在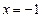 时有极大值
时有极大值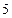 (用求导的方法),
(用求导的方法),
且在端点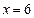 处的值为
处的值为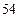 .
.
∴函数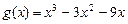 (
(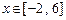 )的最大值为
)的最大值为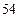 .
.
所以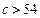 .
.
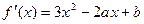 ,设切点为
,设切点为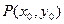 ,则曲线
,则曲线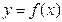 在点P的切线的斜率
在点P的切线的斜率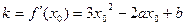 ,由题意知
,由题意知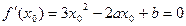 有解,
有解,∴
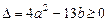 即
即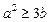 .
.(2)若函数
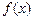 可以在
可以在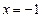 和
和 时取得极值,
时取得极值,则
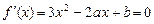 有两个解
有两个解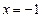 和
和 ,且满足
,且满足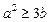 .
. 易得
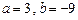 .
. (3)由(2),得
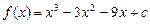 .
. 根据题意,
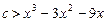 (
(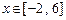 )恒成立.
)恒成立. ∵函数
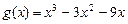 (
(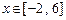 )在
)在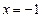 时有极大值
时有极大值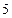 (用求导的方法),
(用求导的方法),且在端点
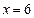 处的值为
处的值为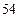 .
. ∴函数
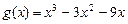 (
(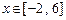 )的最大值为
)的最大值为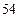 .
. 所以
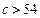 .
. 
练习册系列答案
相关题目
 .
. 在x = 0处取得极值为 – 2,求a、b的值;
在x = 0处取得极值为 – 2,求a、b的值;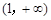 上是增函数,求实数a的取值范围.
上是增函数,求实数a的取值范围.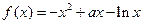 (
(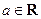 ).
).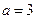 时,求函数
时,求函数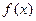 在
在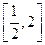 上的最大值和最小值;
上的最大值和最小值;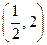 单调时,求
单调时,求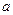 的取值范围;
的取值范围;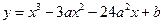 有正的极大值和负的极小值,其差为4,
有正的极大值和负的极小值,其差为4,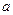 的值;
的值;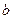 的取值范围.
的取值范围.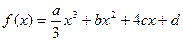 的图象关于原点对称,
的图象关于原点对称,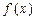 的图象在点
的图象在点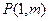 处的切线的斜率为
处的切线的斜率为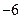 ,且当
,且当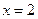 时
时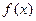 有极值.
有极值.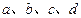 的值;
的值; 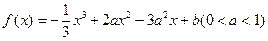
 ,求a的取值范围.
,求a的取值范围.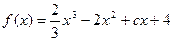 ,
,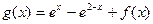 ,
,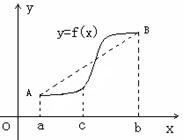
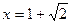 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间;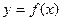 的图象在
的图象在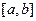 连续光滑,试猜想拉格朗日中值定理:即一定存在
连续光滑,试猜想拉格朗日中值定理:即一定存在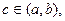 使得
使得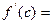 ?(用含有a,b,f(a),f(b)的表达式直接回答)
?(用含有a,b,f(a),f(b)的表达式直接回答)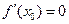 时,
时,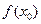 为
为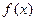 的极大值
的极大值