题目内容
12.计算:sin30°+sin(30°+120°)+sin(30°+240°),
sin60°+sin(60°+120°)+sin(60°+240°).
观察以上两式及其结果的特点,请写出一个一般的等式,使得上述两式为它的一个特例,并证明你写的结论.
分析 利用特殊角的三角函数进行计算,借助于和(差)角的三角函数公式进行证明即可.
解答 解:sin30°+sin(30°+120°)+sin(30°+240°)=$\frac{1}{2}+\frac{1}{2}$-1=0,
sin60°+sin(60°+120°)+sin(60°+240°)=$\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}$=0.
一般的等式:sinα+sin(α+120°)+sin(α+240°)=0
证明:左边=sinα+sin(α-120°)+sin(α+240°)=sinα-$\frac{1}{2}$sinα+$\frac{\sqrt{3}}{2}$cosα-$\frac{1}{2}$sinα-$\frac{\sqrt{3}}{2}$cosα=0
点评 本题考查归纳推理,考查三角函数知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
4.点P(x0,y0)在直线l:f(x,y)=0外,则l1:f(x,y)+f(x0,y0)=0与l2:f(-y,x)+f(x0,y0)=0的位置关系是( )
| A. | 平行 | B. | 垂直 | C. | 平行或重合 | D. | 相交且不垂直 |
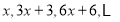 的第四项等于( )
的第四项等于( )