题目内容
【题目】已知圆N经过点A(3,1),B(﹣1,3),且它的圆心在直线3x﹣y﹣2=0上.
(Ⅰ)求圆N的方程;
(Ⅱ)求圆N关于直线x﹣y+3=0对称的圆的方程.
(Ⅲ)若点D为圆N上任意一点,且点C(3,0),求线段CD的中点M的轨迹方程.
【答案】解:(Ⅰ)由已知可设圆心N(a,3a﹣2),又由已知得|NA|=|NB|,
从而有 ![]() =
= ![]() ,解得:a=2.
,解得:a=2.
于是圆N的圆心N(2,4),半径r= ![]() .
.
所以,圆N的方程为(x﹣2)2+(y﹣4)2=10.
(Ⅱ)N(2,4)关于x﹣y+3=0的对称点为(1,5),
所以圆N关于直线x﹣y+3=0对称的圆的方程为(x﹣1)2+(y﹣5)2=10
(Ⅲ)设M(x,y),D(x1 , y1),则由C(3,0)及M为线段CD的中点得: 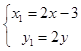 .
.
又点D在圆N:(x﹣2)2+(y﹣4)2=10上,所以有(2x﹣3﹣2)2+(2y﹣4)2=10,
化简得: ![]() .
.
故所求的轨迹方程为 ![]()
【解析】(Ⅰ)首先设出方程,将点坐标代入得到关于参数的方程组,通过解方程组得到参数值,从而确定其方程;(Ⅱ)求出N(2,4)关于x﹣y+3=0的对称点为(1,5),即可得到圆N关于直线x﹣y+3=0对称的圆的方程;(Ⅲ)首先设出点M的坐标,利用中点得到点D坐标,代入圆的方程整理化简得到的中点M的轨迹方程.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】某地区为了解70﹣80岁的老人的日平均睡眠时间(单位:h),随机选择了50位老人进行调查,下表是这50位老人睡眠时间的频率分布表:
序号i | 分组 | 组中值(Gi) | 频数 | 频率(Fi) |
1 | [4,5) | 4.5 | 6 | 0.12 |
2 | [5,6) | 5.5 | 10 | 0.20 |
3 | [6,7) | 6.5 | 20 | 0.40 |
4 | [7,8) | 7.5 | 10 | 0.20 |
5 | [8,9] | 8.5 | 4 | 0.08 |
在上述统计数据的分析中一部分计算见算法流程图,则输出的S的值为 . 