Question

【题目】我们把焦点相同，且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”．已知F1、F2是一对相关曲线的焦点，P是它们在第一象限的交点，当∠F1PF2=60°时，这一对相关曲线中双曲线的离心率是（　　）
A.
B.
C.
D.2

Answer 1

【答案】A
【解析】设F1P=m，F2P=n，F1F2=2c，
由余弦定理得（2c）2=m2+n2﹣2mncos60°，
即4c2=m2+n2﹣mn，
设a1是椭圆的长半轴，a2是双曲线的实半轴，
由椭圆及双曲线定义，得m+n=2a1 ， m﹣n=2a2 ，
∴m=a1+a2 ， n=a1﹣a2 ，
将它们及离心率互为倒数关系代入前式得3a22﹣4c2+=0，
a1=3a2 ， e1e2=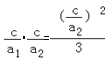=1，
解得e2= ．
故选A．
设F1P=m，F2P=n，F1F2=2c，由余弦定理4c2=m2+n2﹣mn，设a1是椭圆的长半轴，a1是双曲线的实半轴，由椭圆及双曲线定义，得m+n=2a1 ， m﹣n=2a2 ， 由此能求出结果．