题目内容
【题目】如图,P为⊙O外一点,PC交⊙O于F,C,PA切⊙O于A,B为线段PA的中点,BC交⊙O于D,线段PD的延长线与⊙O交于E,连接FE.求证:
(Ⅰ)△PBD∽△CBP;
(Ⅱ)AP∥FE.
【答案】证明:(Ⅰ)如图,∵PA切⊙O于A,∴BA2=BDBC,
∵B为线段PA的中点,∴PB=BA,
∴PB2=BDBC,即![]() ,
,
∵∠PBD=∠CBP,∴△PBD∽△CBP.
(Ⅱ)∵△PBD∽△CBP,∴∠BPD=∠C,
∵∠C=∠E,∴∠BPD=∠E,
∴AP∥FE.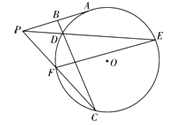
【解析】(Ⅰ)由切割线定理得BA2=BDBC,从而PB2=BDBC,由此能证明△PBD∽△CBP.
(Ⅱ)由三角形相似得∠BPD=∠C,从而∠BPD=∠E,由此能证明AP∥FE.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目