题目内容

正三棱锥的高为
3
，侧棱长为
7
，那么侧面与底面所成二面角的大小是（　　）
A．60°B．30°C．arccos
21
7
D．arcsin
21
7
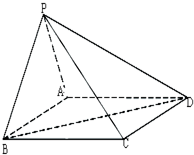
设正三棱锥为P-ABC，底面为正三角形，高OP，O点为△ABC外（内心、重心），OC=
PC2-OP2
=2 延长CO交AB于D，OD=
OC
2
=1，CD=3，BD=
3
，
PD=
OP2+OD2
=2，AB⊥CD，PD⊥AB，∠CDP是P-AB-C二面角的平面角，
cos∠CDP=
1
2
，∠CDP=60°，是侧面与底面所成的二面角．
故选：A
练习册系列答案
相关题目
在直角坐标系中，A（-2，3），B（3，-2）沿x轴把直角坐标系折成90°的二面角，则此时线段AB的长度为（　　）
A．2
5
B．
38
C．5
2
D．4
2
正四棱柱ABCD-A1B1C1D1中，底面边长为a，侧棱AA1长为ka（k＞0），E为侧棱BB1的中点，记以AD1为棱，EAD1，A1AD1为面的二面角大小为θ．
（1）是否存在k值，使直线AE⊥平面A1D1E，若存在，求出k值；若不存在，说明理由；
（2）试比较tanθ与2
2
的大小．
如图，在四棱锥P-ABCD中，底面ABCD是矩形，知AB=3，AD=2，PA=2，PD=2
2
，∠PAB=60°．
（1）证明：AD⊥平面PAB；
（2）求异面直线PC与AD所成的角的余弦值；
（3）求二面角P-BD-A的大小余弦值．
如图，在边长为2的正方形ABCD中，点E是AB的中点，点F是BC的中点，将△AED，△CDF分别沿DE，DF折起，使A，C两点重合于A′．

（1）求证：A′D⊥EF；
（2）求二面角A′-EF-D的正切值．
长方体ABCD-A1B1C1D1的侧棱AA1=a，底面ABCD的边长AB=2a，BC=a，E为C1D1的中点；
（1）求证：DE⊥平面BCE；
（2）求二面角E-BD-C的正切值．
如图，P是二面角α-AB-β棱AB上的一点，分别在α，β上引射线PM，PN，如果∠BPM=∠BPN=45°，∠MPN=60°，那么二面角α-AB-β的大小是 ______．
已知在三棱锥S-ABC中，底面是边长为4的正三角形，侧面SAC⊥底面ABC，M，N分别是AB，SB的中点，SA=SC=2
3
：
（1）求证AC⊥SB
（2）求二面角N-CM-B的大小
（3）求点B到面CMN的距离．
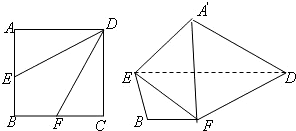
将边长为的正方形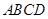沿对角线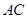折起，使得平面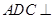平面，   
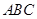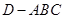在折起后形成的三棱锥中，给出下列三个命题：
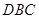①面是等边三角形； ②； 
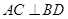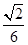③三棱锥的体积是.
其中正确命题的序号是_          .（写出所有正确命题的序号）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网