题目内容
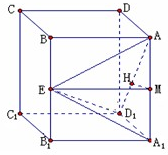
正四棱柱ABCD-A1B1C1D1中,底面边长为a,侧棱AA1长为ka(k>0),E为侧棱BB1的中点,记以AD1为棱,EAD1,A1AD1为面的二面角大小为θ.
(1)是否存在k值,使直线AE⊥平面A1D1E,若存在,求出k值;若不存在,说明理由;
(2)试比较tanθ与2
的大小.
(1)是否存在k值,使直线AE⊥平面A1D1E,若存在,求出k值;若不存在,说明理由;
(2)试比较tanθ与2
| 2 |

(1)存在k=2,使得AE⊥平面A1D1E
证明:若AE⊥平面A1D1E,则AE⊥A1E,于是AE2+A1E2=AA12,
即2[a2+(
)2]=(ka)2,解得k=2,
∴存在k=2,使得AE⊥平面A1D1E.
(2)取A1A中点M,连接EM,在正四棱柱AC1中,EM⊥平面ADD1A1,过M作MH⊥AD1于H,连接EH,则∠MHE为二面角E-AD1-A1的平面角,即∠MHE=θ,
在Rt△AA1D1中,
=
,即MH=
在Rt△EMH中,tanθ=
=2
,
当0<k<1时,tanθ>2
;
当k=1时,tanθ=2
;
当k>1时,tanθ<2

证明:若AE⊥平面A1D1E,则AE⊥A1E,于是AE2+A1E2=AA12,
即2[a2+(
| ka |
| 2 |
∴存在k=2,使得AE⊥平面A1D1E.
(2)取A1A中点M,连接EM,在正四棱柱AC1中,EM⊥平面ADD1A1,过M作MH⊥AD1于H,连接EH,则∠MHE为二面角E-AD1-A1的平面角,即∠MHE=θ,
在Rt△AA1D1中,
| MH |
| A1D1 |
| AM |
| AD1 |
| ka | ||
2
|
在Rt△EMH中,tanθ=
| EM |
| MH |
1+
|
当0<k<1时,tanθ>2
| 2 |
当k=1时,tanθ=2
| 2 |
当k>1时,tanθ<2
| 2 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目