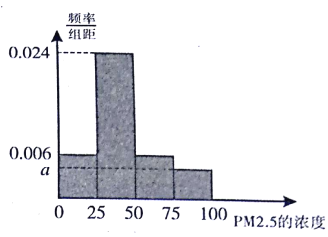
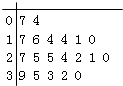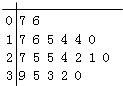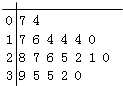题目内容
【题目】已知数列{an}的前n项和Sn= 
n，
（1）求通项公式an的表达式；
（2）令bn=an2n﹣1 ， 求数列{bn}的前n项的和Tn ．
【答案】
（1）解：当n≥2时，an=Sn﹣Sn﹣1= 
n﹣ 
（n﹣1）2﹣ （n﹣1）=n，
当n=1时，a1=S1=1也适合上式，
∴通项公式an的表达式为an=n
（2）解：bn=an2n﹣1=n2n﹣1，
∴Tn=120+2×21+…+（n﹣1）2n﹣2+n2n﹣1①
2Tn=121+222+…+（n﹣1）2n﹣1+n2n②
②﹣①得到，Tn=﹣（120+121+…+12n﹣1）+n2n=（n﹣1）2n+1
所以Tn=（n﹣1）2n+1
【解析】（1）因为给出了数列{an}的前n项和Sn= n，所以可用n≥2时，an=Sn﹣Sn﹣1来求数列{an}的通项公式，再判断n=1是否符合通项公式即可．（2）把（1）中求出的数列{an}的通项公式代入bn=an2n﹣1 ， 求出数列{bn}的通项公式，再利用错位相减法求数列{bn}的前n项和Tn ．
【考点精析】解答此题的关键在于理解等差数列的通项公式（及其变式）的相关知识，掌握通项公式：
或
，以及对等差数列的前n项和公式的理解，了解前n项和公式：
．
练习册系列答案
相关题目
