题目内容
若点O和点F分别为椭圆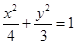 的中心和左焦点,点P为椭圆上的任意一点,则
的中心和左焦点,点P为椭圆上的任意一点,则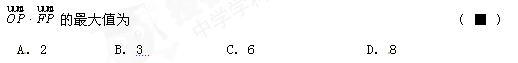
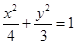 的中心和左焦点,点P为椭圆上的任意一点,则
的中心和左焦点,点P为椭圆上的任意一点,则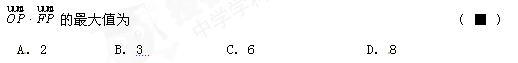
C
先求出左焦点坐标F,设P(x0,y0),根据P(x0,y0)在椭圆上可得到x0、y0的关系式,表示出向量  、
、  ,根据数量积的运算将x0、y0的关系式代入组成二次函数进而可确定答案.
,根据数量积的运算将x0、y0的关系式代入组成二次函数进而可确定答案.
解答:解:由题意,F(-1,0),设点P(x0,y0),则有 ,解得y02=3(1-
,解得y02=3(1- ),
),
因为 =(x0+1,y0),
=(x0+1,y0), =(x0,y0),
=(x0,y0),
所以 ?
? =x0(x0+1)+y02=
=x0(x0+1)+y02= ?
? =x0(x0+1)+3(1-
=x0(x0+1)+3(1- )=
)= +x0+3,
+x0+3,
此二次函数对应的抛物线的对称轴为x0=-2,
因为-2≤x0≤2,所以当x0=2时, ?
? 取得最大值
取得最大值 ,
,
故选C.
 、
、  ,根据数量积的运算将x0、y0的关系式代入组成二次函数进而可确定答案.
,根据数量积的运算将x0、y0的关系式代入组成二次函数进而可确定答案.解答:解:由题意,F(-1,0),设点P(x0,y0),则有
 ,解得y02=3(1-
,解得y02=3(1- ),
),因为
 =(x0+1,y0),
=(x0+1,y0), =(x0,y0),
=(x0,y0),所以
 ?
? =x0(x0+1)+y02=
=x0(x0+1)+y02= ?
? =x0(x0+1)+3(1-
=x0(x0+1)+3(1- )=
)= +x0+3,
+x0+3,此二次函数对应的抛物线的对称轴为x0=-2,
因为-2≤x0≤2,所以当x0=2时,
 ?
? 取得最大值
取得最大值 ,
,故选C.

练习册系列答案
相关题目
 )是椭圆E:
)是椭圆E: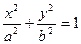 (
(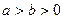 )上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.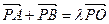 (0<λ<4,且λ≠2).求证:直线AB的斜率等于椭圆E的离心率;
(0<λ<4,且λ≠2).求证:直线AB的斜率等于椭圆E的离心率;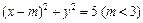 与椭圆E:
与椭圆E: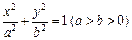
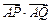 的取值范围.
的取值范围.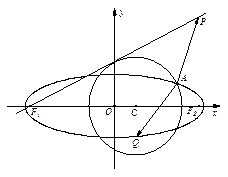 w.
w. 个焦点
个焦点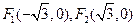 ,过
,过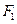 且与坐标轴不平行的直线
且与坐标轴不平行的直线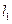 与椭圆相交于M,N两点,如果
与椭圆相交于M,N两点,如果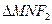 的周长等于8.
的周长等于8.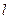 与椭圆交于不同两点P、Q,试问在
与椭圆交于不同两点P、Q,试问在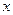 轴上是否存在定点E(
轴上是否存在定点E(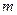 ,0),使
,0),使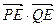 恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.
恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.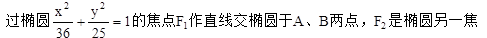 点,则△ABF2的周长是
点,则△ABF2的周长是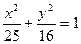 的离心率为
的离心率为 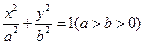 ,A(2,0)为椭圆与X轴的一个交点,过原点O的直线交椭圆于B、C两点,且
,A(2,0)为椭圆与X轴的一个交点,过原点O的直线交椭圆于B、C两点,且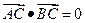 ,
,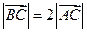
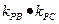 是否为定值?若是定值,求出该定值;若不是定值,请说明理由。
是否为定值?若是定值,求出该定值;若不是定值,请说明理由。
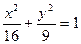 的两焦点分别为F1、F2,过F1作直线交椭圆于A、B两点,
的两焦点分别为F1、F2,过F1作直线交椭圆于A、B两点,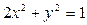 的顶点为焦点,以椭圆的焦点为顶点的双曲线方程为
的顶点为焦点,以椭圆的焦点为顶点的双曲线方程为