题目内容
12.已知不共线向量$\overrightarrow{a}$,$\overrightarrow{b}$,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$的夹角是( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
分析 根据向量的三角形法则,结合向量的几何意义,画图即可得到答案.
解答 解:如图,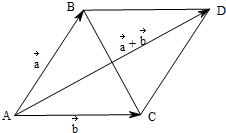 ∵不共线向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,
∵不共线向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,
∴以$\overrightarrow{a},\overrightarrow{b}$为邻边的平行四边形为菱形
且∠BAC=$\frac{π}{3}$,
则$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$的夹角为∠BAD=$\frac{π}{6}$.
故选:B.
点评 本题主要考查向量的夹角的求解,利用向量加减法的几何意义求解是解决该题的关键,是基础题.

练习册系列答案
相关题目
4.从1,2,2,3,3,3这六个数字中任取5个,组成五位数,则不同的五位数共有( )
| A. | 50个 | B. | 60个 | C. | 100个 | D. | 120个 |
8.等差数列{an}的前n项和为Sn,且a1+a2=10,S4=36,则过点P(n,an)和Q(n+2,an+2)(n∈N*)的直线的一个方向向量是( )
| A. | $(-\frac{1}{2},-2)$ | B. | (-1,-1) | C. | $(-\frac{1}{2},-1)$ | D. | (2,$\frac{1}{2}$) |
17.已知圆(x+1)2+y2=4的圆心为C,点P是直线l:mx-y-5m+4=0上的点,若该圆上存在点Q使得∠CPQ=30°,则实数m的取值范围为( )
| A. | [-1,1] | B. | [-2,2] | C. | $[{\frac{{\sqrt{3}-3}}{4},\frac{{\sqrt{3}+3}}{4}}]$ | D. | $[{0,\frac{12}{5}}]$ |
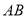 是
是 的直径,
的直径,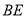 为
为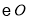 的切线,点
的切线,点 为
为 上不同于
上不同于 、
、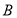 的一点,
的一点, 为
为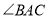 的平分线,且分别与
的平分线,且分别与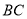 交于
交于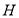 ,与
,与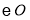 交于
交于 ,与
,与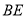 交于
交于 ,连接
,连接 、
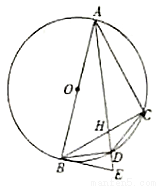
、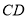 .
.
 ;
; .
.