函数f(x)=$\left\{\begin{array}{l}{x.当x≥1}\\{0.当x=0}\\{-1.当x＜-1}\end{array}\right.$的值域是{0}∪{-1}∪[1.+∞)．题目和参考答案——青夏教育精英家教网——

题目内容

2．函数f（x）=$\left\{\begin{array}{l}{x，当x≥1}\\{0，当x=0}\\{-1，当x＜-1}\end{array}\right.$的值域是{0}∪{-1}∪[1，+∞）．

分析根据函数的解析式进行求解即可．

解答解：当x≥1时，f（x）=x≥1，
当x=0时，f（x）=0，
当x＜-1时，f（x）=-1，
故函数的值域为{0}∪{-1}∪[1，+∞），
故答案为：{0}∪{-1}∪[1，+∞）

点评本题主要考查函数值域的求解，根据分段函数的表达式分别求出取值范围是解决本题的关键．

练习册系列答案

悦然好学生单元练系列答案

实验班提优课堂系列答案

英才考评系列答案

课堂练加测系列答案

百分百训练系列答案

新体验课时训练系列答案

尖子班系列答案

高分拔尖课时作业系列答案

轻松课堂单元测试AB卷系列答案

南通小题课时提优作业本系列答案

相关题目

12．已知等比数列{b_n}前n项和为S_n=3ⁿ-k（k∈R），公差为k的等差数列{a_n}，满足b₁=a₁．
（Ⅰ）求数列{a_n}，{b_n}的通项公式；
（Ⅱ）设c_n=$\frac{（2{a}_{n}-1）{b}_{n+2}}{2{a}_{n}{a}_{n+1}}$，求数列{c_n}，的前n项和T_n．

13．已知函数f（x）=$\frac{lnx}{x}$（x＞0）．
（Ⅰ）求f（x）的单调区间和极值；
（Ⅱ）若m＞n＞0，讨论mⁿ与n^m的大小关系并给出证明．

10．已知数列{a_n}的前n项和为S_n，若a_n=$\frac{1}{{\sqrt{n}+\sqrt{n+1}}}$，S_n=10，则n=（　　）

17．已知△ABC中，3a²-2ab+3b²-3c²=0，则cosC=$\frac{1}{3}$．

7．（1+i）²⁰-（1-i）²⁰的值为（　　）

14．不等式x（x+2）≥0的解集为（　　）

{x|x≥0或x≤-2}

{x|x≤0或x≥2}

11．已知$\overrightarrow{a}$=（-3，2），$\overrightarrow{b}$=（2，1），$\overrightarrow{c}$=（3，-1），t∈R，若$\overrightarrow{a}$-t$\overrightarrow{b}$与$\overrightarrow{c}$共线，则实数t=$\frac{3}{5}$．

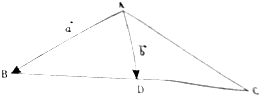如图，在△ABC中，D为BC中点，记$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，已知|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=1，＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=$\frac{π}{3}$．
（1）用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{AC}$．
（2）求|$\overrightarrow{AC}$|