题目内容
【题目】若数列![]() 、
、![]() 满足
满足![]() (
(![]() N*),则称
N*),则称![]() 为数列
为数列![]() 的“偏差数列”.
的“偏差数列”.
(1)若![]() 为常数列,且为
为常数列,且为![]() 的“偏差数列”,试判断
的“偏差数列”,试判断![]() 是否一定为等差数列,并说明理由;
是否一定为等差数列,并说明理由;
(2)若无穷数列![]() 是各项均为正整数的等比数列,且
是各项均为正整数的等比数列,且![]() ,
,![]() 为数列
为数列![]() 的“偏差数列”,求
的“偏差数列”,求![]() 的值;
的值;
(3)设![]() ,
,![]() 为数列
为数列![]() 的“偏差数列”,
的“偏差数列”,![]() ,
,![]() 且
且![]() ,若
,若![]() 对任意
对任意![]() 恒成立,求实数M的最小值.
恒成立,求实数M的最小值.
【答案】(1)见解析;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1){an}不一定为等差数列,如![]() ;
;
(2)设数列{an}的公比为q,解方程可得首项和公比,由等比数列的通项公式和求和公式,计算可得所求值;
(3)由累加法可得数列{an}的通项公式,讨论n为奇数或偶数,求得极限,由不等式恒成立思想可得M的最小值.
解:(1) 如![]() ,则
,则![]() 为常数列,但
为常数列,但![]() 不是等差数列,
不是等差数列,
(2) 设数列![]() 的公比为
的公比为![]() ,则由题意,
,则由题意,![]() 、
、![]() 均为正整数,
均为正整数,
因为![]() ,所以
,所以![]() ,
,
解得![]() 或
或![]() ,
,
故![]() 或
或![]() (
(![]() N*),
N*),
①当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
② 当![]() 时,
时,![]() ,
,![]() ,
,![]()
综上,![]() 的值为
的值为![]() 或
或![]() ;
;
(3) 由![]() ≤
≤![]() 且
且![]() ≤
≤![]() 得,
得,![]() =
=![]()
故有:![]() ,
,
![]() ,
,
![]() ,
,
累加得: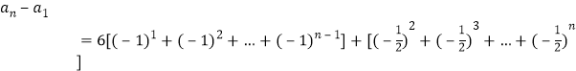
=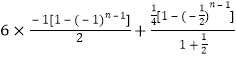
=![]() ,
,
又![]() ,所以
,所以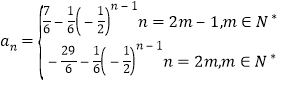
当n为奇数时,![]() 单调递增,
单调递增,![]() ,
,![]() ,
,
当n为偶数时,![]() 单调递减,
单调递减,![]() ,
,![]() ,
,
从而![]() ≤
≤![]() ,所以M≥
,所以M≥![]() ,即M的最小值为
,即M的最小值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】省环保厅对![]() 、
、![]() 、
、![]() 三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
|
|
| |
优(个) | 28 |
|
|
良(个) | 32 | 30 |
|
已知在这180个数据中随机抽取一个,恰好抽到记录![]() 城市空气质量为优的数据的概率为0.2.
城市空气质量为优的数据的概率为0.2.
(1)现按城市用分层抽样的方法,从上述180个数据中抽取30个进行后续分析,求在![]() 城中应抽取的数据的个数;
城中应抽取的数据的个数;
(2)已知![]() ,
, ![]() ,求在
,求在![]() 城中空气质量为优的天数大于空气质量为良的天数的概率.
城中空气质量为优的天数大于空气质量为良的天数的概率.