题目内容
设椭圆C∶ +
+ =1(a>b>0)过点(0,4),离心率为
=1(a>b>0)过点(0,4),离心率为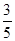 .
.
(1)求C的方程;
(2)求过点(3,0)且斜率为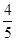 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.
 +
+ =1(a>b>0)过点(0,4),离心率为
=1(a>b>0)过点(0,4),离心率为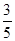 .
.(1)求C的方程;
(2)求过点(3,0)且斜率为
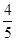 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.(1)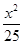 +
+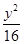 =1;(2) (
=1;(2) (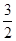 ,-
,-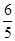 ).
).
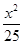 +
+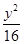 =1;(2) (
=1;(2) (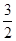 ,-
,-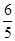 ).
).试题分析:(1)由已知可得b=4,再由在椭圆中有:
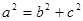 及离心率
及离心率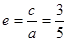 ,可求得a的值,从而就可写出椭圆C的方程;(2)由已知可写出过点(3,0)且斜率为
,可求得a的值,从而就可写出椭圆C的方程;(2)由已知可写出过点(3,0)且斜率为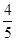 的直线方程,将此直线方程代入椭圆C的方程中,解此方程就可求得直线被C所截线段的两个端点的横坐标,从而求得线段中点的横坐标,再代入直线方程就可得到线段中点的纵坐标,若方程不好解,注意韦达定理可直接求得所求线段中点的横坐标,进而可得线段中点的坐标.
的直线方程,将此直线方程代入椭圆C的方程中,解此方程就可求得直线被C所截线段的两个端点的横坐标,从而求得线段中点的横坐标,再代入直线方程就可得到线段中点的纵坐标,若方程不好解,注意韦达定理可直接求得所求线段中点的横坐标,进而可得线段中点的坐标.试题解析:(1)将(0,4)代入C的方程得
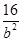 =1,∴b=4,
=1,∴b=4,由e=
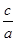 =
=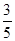 得
得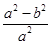 =
=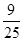 ,即1-
,即1-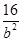 =
=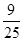 ,∴a=5,∴C的方程为
,∴a=5,∴C的方程为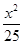 +
+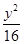 =1.
=1.(2)过点(3,0)且斜率为
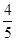 的直线方程为 y =
的直线方程为 y =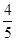 (x-3),设直线与C的交点为A(x1,y1),B(x2,y2),将直线方程y=
(x-3),设直线与C的交点为A(x1,y1),B(x2,y2),将直线方程y=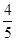 (x-3)代入C的方程,得
(x-3)代入C的方程,得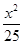 +
+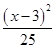 =1,即x2-3x-8=0,解得
=1,即x2-3x-8=0,解得x1=
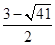 ,x2=
,x2=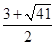 ,
,∴AB的中点坐标
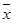 =
=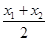 =
=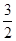 ,
, =
=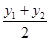 =
=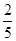 (x1+x2-6)=-
(x1+x2-6)=-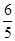 ,
,即中点坐标为(
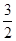 ,-
,-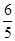 ).
).
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 交于A、B两点,记△AOB的面积为S(O是坐标原点).
交于A、B两点,记△AOB的面积为S(O是坐标原点).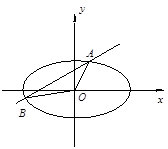
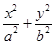 =1(a>0,b>0)的离心率与双曲线
=1(a>0,b>0)的离心率与双曲线 =1的一条渐近线的斜率相等以原点为圆心,椭圆的短半轴长为半径的圆与直线sin
=1的一条渐近线的斜率相等以原点为圆心,椭圆的短半轴长为半径的圆与直线sin ·x+cos
·x+cos (O为坐标原点),当
(O为坐标原点),当 时,求实数t取值范围.
时,求实数t取值范围. :
: 和
和 :
: 的焦点分别为
的焦点分别为 、
、 ,点
,点 是
是 的形状是( )
的形状是( ) 的焦点的直线
的焦点的直线 与抛物线交于
与抛物线交于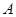 、
、 两点,且
两点,且 (
( 为坐标原点)的面积为
为坐标原点)的面积为 ,则
,则 = .
= .