题目内容
【题目】如图,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)详见解析;(2) ![]() ;(3)
;(3)![]()
【解析】
试题分析:(Ⅰ)取BC中点G点,连接AG,FG,由F,G分别为DC,BC中点,知![]() 且
且![]() ,又AE∥BD且
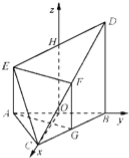
,又AE∥BD且![]() ,故AE∥FG且AE=FG,由此能够证明EF⊥平面BCD.(Ⅱ)取AB的中点O和DE的中点H,分别以OC、OB、OH所在直线为x、y、z轴建立如图空间直角坐标系,则
,故AE∥FG且AE=FG,由此能够证明EF⊥平面BCD.(Ⅱ)取AB的中点O和DE的中点H,分别以OC、OB、OH所在直线为x、y、z轴建立如图空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() .求出面CDE的法向量
.求出面CDE的法向量![]() ,面ABDE的法向量
,面ABDE的法向量![]() ,由此能求出二面角
,由此能求出二面角![]() 的大小.(Ⅲ)由面CDE的法向量
的大小.(Ⅲ)由面CDE的法向量![]() ,
,![]() ,利用向量法能求出点A到平面CDE的距离.
,利用向量法能求出点A到平面CDE的距离.
试题解析:解:⑴取![]() 中点
中点![]() 点,连接
点,连接![]() 、
、![]() ,
,
∵![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点,∴
中点,∴![]() 且
且![]() ,又
,又![]() 且
且![]() .
.
∴![]() 且
且![]() ,∴四边形
,∴四边形![]() 为平行四边形,则
为平行四边形,则![]() ,
,
∵![]() 平面
平面![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,
,
∵![]() 为
为![]() 中点,且
中点,且![]() ,∴
,∴![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
⑵取![]() 的中点
的中点![]() 和
和![]() 的中点
的中点![]() ,
,
分别以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 、
、![]() 、
、![]() 轴建立如图空间直角坐标系,
轴建立如图空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() , 设面
, 设面![]() 的法向量
的法向量![]() ,
,
则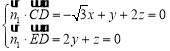 ,取
,取![]() ,
,
取面![]() 的法向量
的法向量![]() ,
,
由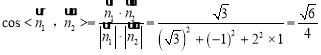 ,
,
故二面角![]() 的大小为
的大小为![]() .
.
⑶由⑵,面![]() 的法向量
的法向量![]() ,
,![]()
![]() ,
,
则点![]() 到平面
到平面![]() 的距离,
的距离,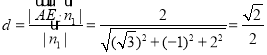 ..
..

 阅读快车系列答案
阅读快车系列答案【题目】为贯彻落实教育部等![]() 部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定举行春季校园足球联赛,为迎接此次联赛,甲中学选拔了
部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定举行春季校园足球联赛,为迎接此次联赛,甲中学选拔了![]() 名学生组成集训队,现统计了这
名学生组成集训队,现统计了这![]() 名学生的身高,记录如下表:
名学生的身高,记录如下表:
身高 |
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
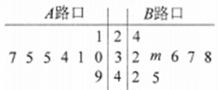
(1)请计算这![]() 名学生的身高中位数、众数,并补充完成下面的茎叶图:
名学生的身高中位数、众数,并补充完成下面的茎叶图:

(2)身高为![]() 和
和![]() 的四名学生分别为
的四名学生分别为![]() ,现从这四名学生中选
,现从这四名学生中选![]() 名担任正副门将,请利用列举法列出所有可能情况,并求学生
名担任正副门将,请利用列举法列出所有可能情况,并求学生![]() 入选正门将的概率.
入选正门将的概率.
【题目】为了弘扬民族文化,某校举行了“我爱国学,传诵经典”考试,并从中随机抽取了100名考生的成绩(得分均为整数,满分100分)进行统计制表,其中成绩不低于80分的考生被评为优秀生,请根据频率分布表中所提供的数据,用频率估计概率,回答下列问题.
分组 | 频数 | 频率 |
| 5 |
|
|
|
|
| 35 |
|
| 25 |
|
| 15 |
|
合计 | 100 |
|
(Ⅰ)求![]() 的值及随机抽取一考生恰为优秀生的概率;
的值及随机抽取一考生恰为优秀生的概率;
(Ⅱ)按成绩采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在![]() 的概率.
的概率.